Modal analysis is, along with linear static analysis, one of the 2 most common types of FE analysis. If you don’t know about those, you’ll have to review your fea basics. That’s what we’ll do here!
In this short article, I’ll talk about:
- What is modal analysis
- Why it is important to know about it
The difference between static and dynamic analysis
Static analysis means that we are making the assumption that the system we are simulating doesn’t depend on time.
Whatever the time period we observe the system, it will remain always the same.
It implies of course that the loads and boundary conditions don’t depend on time either.
In reality, this is a hypothesis, because every load has to be applied from a time t=0 sec
To take that in account, in static analysis, we just say that the load is applied « infinitely slowly » so there is no discontinuity during the load application.
Now…we can only do static analysis in certain cases where we can effectively do the assumption that the model can be considered as static…
There are cases in which the loading itself (or the system) is dynamic and thus we have to perform a dynamic analysis.
For example:
If you want to analyze an object falling on the ground, this is an impact… you understand intuitively that the reaction of the floor will first not apply when the object is in the air and AS SOON AS the object touches the ground, the reaction of the ground suddenly applies and impact the object. The application of the load is short AND intense. This type of phenomenon is 100% dynamic.
Here is an illustration (pardon my poor drawing skills…):
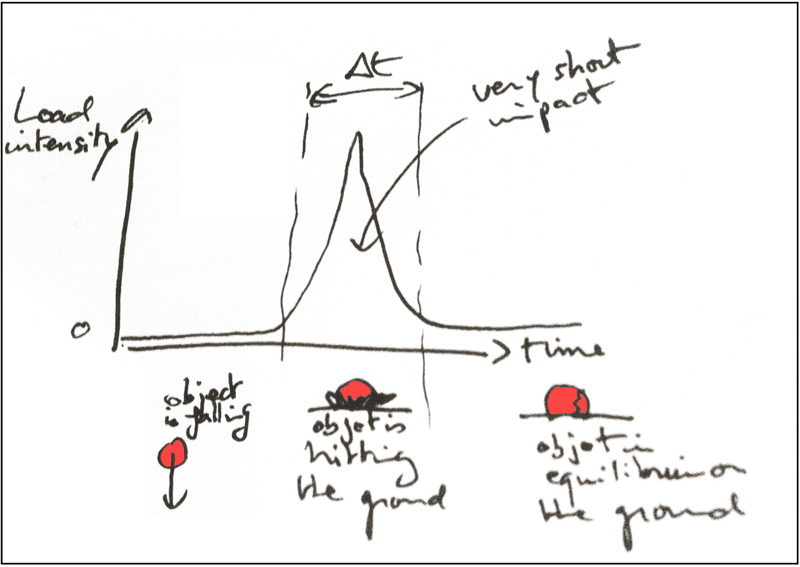
Dynamic Loadings can have various temporal distributions and it definitely has an impact on the system.
To Resume:
- In static analysis, the system and the boundary conditions don’t depend on time. What matters is the intensity of the load.
- In dynamic analysis, there is a time dependency. What matters is the intensity of the load AND the temporal distribution of the loading.
Cyclic loadings (fea basics)
I think that this is generally understood, but a short reminder is always good.
Cyclic loads have a certain frequency, period and intensity.
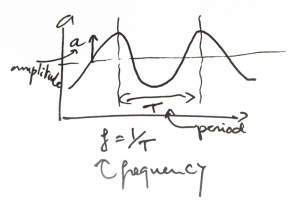
Cyclic loadings are transient loads. If you want to understand more about transient and steady-state and really understand the difference, I wrote another article about the topic in the past here.
The response of mechanical systems to cyclic loadings
To explain things simply, you can say that the response of a system to a dynamic loading can be like the following:
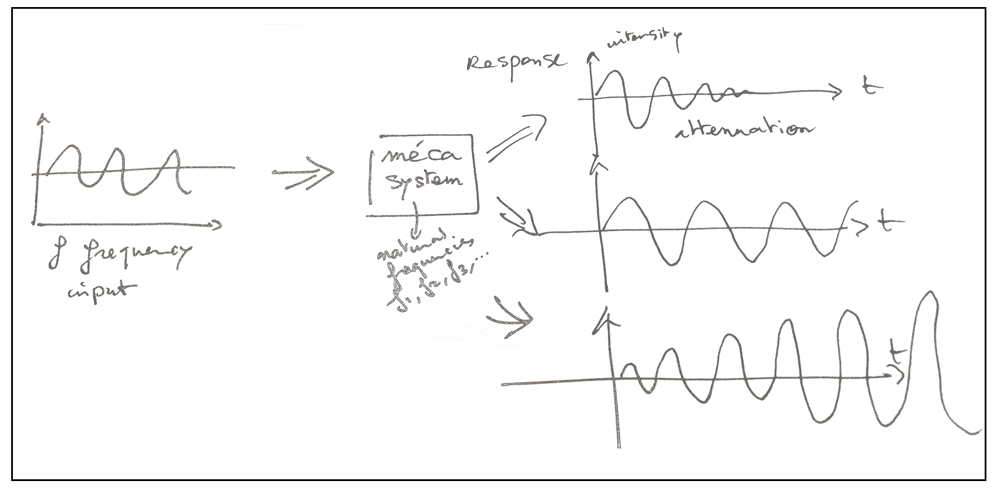
- The intensity of the response can converge
- The system can oscillate
- The intensity of the system can diverge
In all cases, we want to avoid the 3rd type of response, because it means that the system will break
Example:
Consider a kid on a swing.
The swing is the mechanical system and the kid provides a forced excitation input.
If the kid’s excitation load has a frequency which becomes close to the swing’s natural frequency, the swing goes up and up and the oscillations increase.
This phenomenon is called « resonance ».
(You can imagine that if the kid continues to push, he will be ejected—> that’s dangerous ;-) )
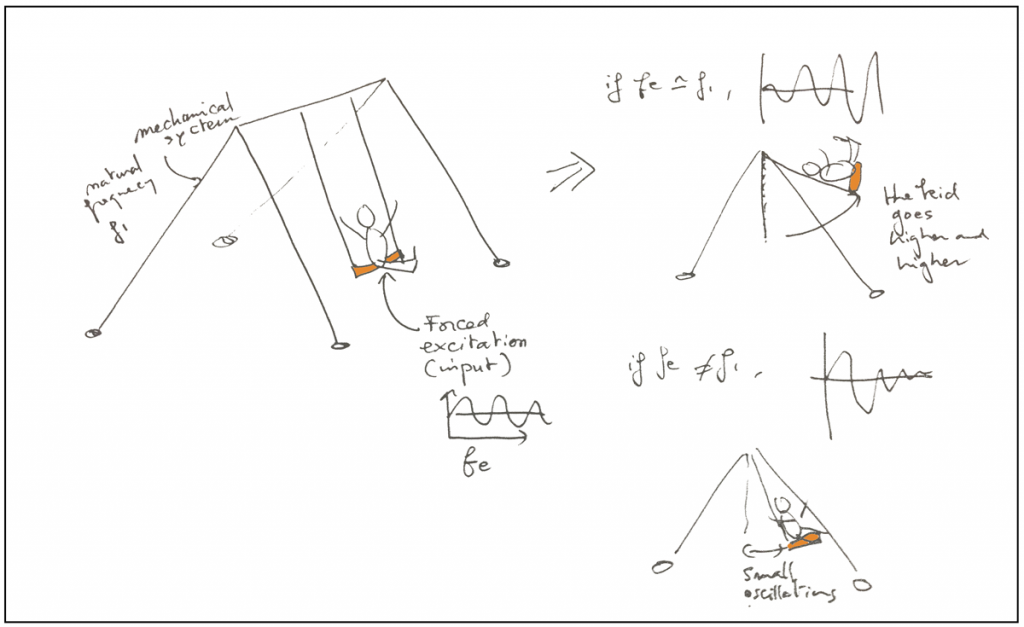
The same can happen for any mechanical system that oscillates or vibrates.
Resonance can be dangerous… and in case you don’t know… bridges have broken like that in the past because the frequency of the wind was matching the natural frequency of the bridge!
Watch this video if you don’t believe me:
When does it happen?
It happens when the system enters in « resonance » with the frequency of the input loading.
Which means:
When the frequency of the input load is equal to the « resonance » frequency of the system.
Now that you know that, you understand that it is absolutely critical to be able to calculate the resonance frequency of a system
—> That’s what Modal analysis does for you! :)
(Note that the « resonance » frequencies and commonly called « natural frequencies » or « mode frequencies »)
So what is modal analysis??
To explain it simply, modal analysis is a simple way to calculate the natural frequencies of your system so you know which frequencies can be destructive and dangerous for it.
Here a video I just created to show you how to perform simple modal analysis:
Why there is no load in a modal analysis?
That’s a question I often get about fea basics
Modal analysis calculates the natural frequencies of the system alone.
Modal is the simplest analysis and the only thing it does is telling you what are the “resonance frequencies” of your geometry. It isn’t related to a loading at this stage, only to the geometry. Resonance frequencies change due to the shape of your model and the way it is constrained only.
Because generally, once you noted the dangerous natural frequencies, you actually want to know:
“If I excite my model at this dangerous frequency, how much deformation will I really get?”
This is done use other types of analysis called « Time response dynamic analysis » or « Frequency response dynamic analysis » fea basics
What is the input I need to provide for the EIGL Card?
Some FEA Software call the input for modal analysis an EIGL Card for fea basics
The EIGRL Card is just a way to enter the parameters for the modal analysis, which are in general:
1- The initial frequency you want to start searching (V1)
2- The last frequency you want to stop searching (V2)
–> You could search the full frequency spectrum but you understand that it is not efficient if you know that you are only interested in the resonance frequencies which are in a certain range
3- The number of modes (N)
–> The modes of vibration are theoretically infinite but generally you only want to get the ones that will lead to the largest deformation
///////////////////////////////////////////////////////////////////////////////////////
Do you like this article? Leave a comment and let me know!
If you are a beginner in FEA simulation, read this article.
Thank you for clear explanation
You’re welcome Manideep! :)
I would actually just like to say a big thank you because even after 4 years I reached this article and it helped me a lot with understanding and performing modal FR analysis. Just massive thanks for your help!
Great Explanation!
Good to know.
Thank you very much for sharing your experience.
Thanks for your explanation :)
Great, presentation is like story telling
Nice and precise
Thanks for the explanation.
Generally we say when the operating frequency match with the natural frequency a resonance is created and component fails. My question is, for an example
The first natural frequency of the component is 18 Hz
And my operating frequency is say 20 Hz.
Will the resonance will be creating???
If it so then why do we are extrating more than one natural frequences.
Kindly explane if i am wrong
Hi Vishnu, you are right… the closer you get to the natural frequency, the stronger will be the response. To know exactly what will be the response, you have to perform a frequency response analysis. Then you will be able to observe and measure the actual response of the system.
WHAT DO YOU MEAN BY NATURAL FREQUENCY OF A BUILDING STRUCTURE?
Like I am describing in the article, each system has natural vibration frequencies…and it includes structures like buildings as well.
one thing puzzles me:
we know from 1st Newton’s law – that every object will remain at rest or in uniform motion in a straight line unless compelled to change its state by the action of an external force.
how come structura can have it’s own frequencies without any external force applied ?
The natural frequencies of a structure describe the response of this structure to loads which are exciting it at those specific frequencies. So 1) With a modal analysis, you understand how the structure would deform when excited, BUT this structure doesn’t really deform until it is actually excited by a force! 2) With a dynamic analysis (Frequency or Time domain) you actually apply a frequency/time dependent load which WILL excite (or not) the natural modes of that structure.
Thanks for the article, it was very much informative.
In continuation to vishnu’s question, If my operating frequency and natural frequency matches, I believe I will have to vary the natural frequency of the system.
In that case, which way should I working towards? (Increase or Decrease).
Which is desirable?
Depends on your system, some system vibrate in low frequency range (for exemple < 50 Hz) and others vibrate at much higher frequencies. You have to choose a span of frequencies which corresponds to the possible vibration range of your system.
The displacements and stresses obtain from model analysis are not realastic. Is it so??
That’s right. Modal analysis doesn’t provide you with this information. It only gives you the mode frequencies and the mode shapes.
I am totally confuse with mode shape.
What exactly meaning of “mode shape”?
At a certain frequency of vibration, your model vibrates in a certain way…at another frequency, it may vibrate too but not in the same way. The mode shape is the hypothetical deformation described by your model at a certain frequency. It is not a real deformation, it is just an idea of how the model would deform while it vibrates at the specific frequency you are looking at.
Consider your output from modal analysis gives you natural frequency of 30Hz and mode shape is bending along y axis,
it says that, If external excitation or alternating load is applied at 30Hz, along y axis , resonance will occur.
How find the vibration velocity (mm/s) of a shatf rotating mixer model?
What do you mean by “Vibration velocity” Samir?
thats was a good explanation
Thank you for your the in depth explanation.
Hey!
This is great!
Also I LOVE the graphics of this article – they are simply awesome :)
Cheers!
Łukasz
Really? I spent 5 min to draw that, haha :)
Simplest solution is the best!
Thanks for your efforts in writing the article. I enjoyed reading it. Every time I read a technical article use to learn something new which I was not aware before, this became true for your article too.
I think that Natural frequencies and Resonance Frequency should be used in different context. Natural frequency is PURELY a structural behavior it’s function of stiffness and mass distribution or in other words function of geometry and support conditions. Loading has no role to play.
If the structure resonate at a particular natural frequency then that frequency is called resonance frequency. A structure can have multiple natural frequencies and their corresponding mode shapes but the structure is not going to resonate at all these natural frequencies. When a natural frequency becomes a resonance frequency depends on the how the external loading ( direction and distribution to excite one or more natural frequencies) is acting on the structure and hence it’s function of loading too.
Though there has been attempts in this article to explain the difference between these two, I think that at some places they are used interchangeably. This shall give a room at some beginner mind to think that they are both one and the same. I learned this from my technical boss after many years of praticing experience.
So in my humble opinion Model analysis mostly the termm Natural frequencies should be used and perhaps at very few places the terms Resonance frequencies can be used to explain when a natural frequency can be called as resonance frequency.
Thanks.
Thanks for your long and interesting comment! You are right :) I kind of simplified a bit the phenomenon to make it better understandable for beginners. There is for sure more to say about it if you want to be rigorous :-) Thanks again for taking the time to explain your thinking!
Dear Cyprien…Real good article…
I just wanted to add something which may look irrelevant wrt this topic but I am finding myself difficult to stop…:))
It is about dynamic analysis you explained above…I worked a lot on dynamic analysis for many different purpose …currently I am using my little knowledge of dynamic analysis for analyzing offshore mechanical structure and full systems…
After multiple years of experience I could easily say it is static analysis which really solves my problem and make me understand deeply what happening in my system. For example I take example from your article above…you mentioned impact of ball on ground. In my personal view dynamic analysis is all about to understand and debate about that critical moment when ball going to hit ground…I mean here that particular moment from whole dynamic analysis is important for me and knowing about what exactly happen to my ball at that time for example if I interested in loads coming on ball. That’s it…….
Now it is my static analysis skills going to help me to understand how ball ( not going too deep on material non linearity ) going to behave because of this impact and how I can improve my design ….blablablaaa:)
Hence I feel doing FEA is more static then dynamic ……In static analysis we understand FEA results deeply….once we understand static then let go to add complexity to problem one by one and understand FEA results individually and later at the end we can combine whole physics togather…
Pl tolerate me guysss because I want to be knowingly ignorant about complex maths people many time confuse me rather talking about solution to engineering..
You are doing real great work….and important you are explaining purpose of doing FEA…In my view whether we structural, CFD, Thermal, Electrical …..Purpose is each physics is improving performance and efficiency of machine/system/subsystem…is not it too simple :))
Best Regards,
Manoj Mittal
mittalmanoj2k@gmail.com
Thank you very much Manoj for your impressive comment and also for sharing your experience here on this article. I believe that sharing experience between engineer is necessary to make progress in this world and I am grateful that you took the time to write your view of the topic.
Okay, this is a bit more advanced sidenote, but I simply cannot leave it unsaid :D Here goes:
I think you can also use the eigenmodes for really lightweight analysis. I mean that once you have the frequency response, you can extract a few of the most significant resonance frequencies (say 3 of them). You can then use those 3 modes to approximate the system response to arbitrary loading.
Not really an expert on this topic, but I did see one demo where they simulated a freaking bridge on a mobile phone using that kind methodology. Impressive, to say the least :O
Hi Antti, I think that you are talking about the modal superposition method right? It’s a good idea to write also about that! Thanks
Errmmm yeah that seems to be the case, based on quick googling :D I had simply used the term “reduced basis” for any method that somehow reduces the number of unknowns for the same mesh :)
Thanks for your valuable share Cyprien.
Have you ever shared any tutorial about rotor dynamics (undamped critical speed analysis, unbalance response analysis, damped eigenvalue analysis and stability analysis)? If not, can you share?
Best Regards,
Talha
Great Article on Modal Analysis. Thank you for that.
Can you write a article on Campbell diagram, which will be plotted once we get the natural frequencies of the system from modal analysis ?
Hi,
I wanted to know difference in modal analysis with constraints and without constraints to understand the natural frequency of the system.
Suppose I have a fixture being mounted on vibration shaker. I can do a modal analysis of it with no constraints and other one with constraints at the mounting locations.
In without constraint case, we get first 6 rigid modes and then actual mode shapes and same is not the case with constraint one.
I have tried both but differences in natural frequency due to boundary condition, which is more useful to avoid the resonance phenomena.
It seems that the constraint one depicts the actual physical thing and no constraint case is generally used as free-free run.
Kindlyl let me know about this.
Thank you.
Hi Gopal, You’re perfectly right! Good luck with your analysis.
Dear Gopal…
I am thinking on this…You do onething next week first thing of your day…open same assembly which was not constrained …in your assembly select any one component which u like most and make loose connection to rest of assembly….now run your modal analysis…pl tell us how many rigid nodes u see in FEA results???
If you see rigid modes more than 6…then it means by running modal analysis you can also find out how many components in ur assembly loosely connected…..
Hureee in case my above observation right…you discovered real practical use of modal analysis and quickly can find for complex assemblies how many components are loosely connected…
Thx Manoj Mittal
mittalmanoj2k@gmail.com
for sinusoidal loading , the knowledge of natural frequencies is must, but what about random loading? how we can predict which mode is dangerous(coz all the frequencies are present all the time). Does mode shape also gives some information,means can we say that this shape can be dangerous?
For random frequency loading, there is a special type of analysis to analyze it called “Random frequency response”. It works basically like a frequency response analysis but with a certain type of random input defined by a certain spectrum distribution that you can define.
Hello Cyprien,
I am new to your website and I am still searching and reading your articles. But can you tell me if you have any article or tutorial made for “Random Frequency Response” analysis? I have been trying to search and understand this topic. If not can you suggest me some material to read? I am a beginner when it comes to dynamic analysis. I have been working on Static FEA for many years now.
Thanks in advance
I am seeing a very nice explanation of Modal analysis.
I am analyzing an ultrasonic horn whose one face is attached with a vertical rotating tool, while other face is attached with transducer.
Now pls tell me should i fix the horn from transducer side for modal analysis, leaving free at rotating tool side.
and what i do for harmonic study.
Hi Amit..
I exactly did not understood your problemmm..It would be really nice if you can share some simple hand images of ur problemmm….but any wayyyy…I can share few common things about structural boundary conditions…
Pl never get messed up with boundary conditions…seriously it is one area in FEA where I personally advise every my fellow FEA friends never ever decide boundary conditions in hurry…let ur boss keep crying but you please take your own time untill your heart and mind understan it completely…This is single most important stuff in FEA and if you go wrong ….consequencies could be really dangerous…
I beleive you are not doing any multibody dynamics…Your aim seems to be doing to confirm first natural frequency of your system…hence your aim should be to identify
1. Most conservative boundary condition
2. To compare real physical condition with ur software bounadry conditions. Example a simple beam both end fixed and you applied vertical load…after running simulation…you should expect displacement/deformation of beam should be downward and no rotation should be at ends…….in case you animation in post shows something diffrently …..which means There is something wrong in your boundary condition…keep correcting your boundary conditions untill you donot see what u wanted to see in post processor…once u happy with ur animations in ur post processor…u win half racee..
3. Also please keep checking reactions and moments looking good..
Just a thought ….May be I am wrong…pl make your own informed decision based on system u seeing in front of ur eyes..
Thx
Manoj Mittal
mittalmanoj2k@gmail.com
Thanks!!! a lot sir for you great help to understand the concept modal analysis…
Hello,
I have two questions
1) Which one should be considered either Free-Free Modal analysis or Constrained modal analysis and Why ?
2) What do you mean by mass participation factor in Modal analysis?
Thanks for your interesting explanation,
I have a question, how many vibration modes is recommended to calculate for a convencional study?
Hi Juan,
What is important is to be able to find the main modes that will impact your specific analysis. More you have modes and more you will have chances that the important modes for you are included inside, but you still have to find which ones. That’s why modal analysis is almost always coupled with another type of analysis such as frequency or time response.
If your structure is simple, then 10 modes should be okay. If you have a more complex system to analyse, you may want to increase your “search for modes”…
Just make sure you have enough modes so that 90 % of effective mass is considered in all direction. Output file will help you to find that.
Juan,
Number of modes to be extracted depends on external excitation frequency if the excitation is harmonic in nature. If you are doing seismic or random vibration analysis you need to make sure that effective mass of the extracted modes is more than 85-90 % of the total mass.
Thanks,
Atul
Nice article
Thanks!!! a lot Cyprien and all the engineers for you great explanation to understand the concept of modal analysis…
Thanks to you Anil! I am glad that this article was useful to you :)
Nice answer….. i have one question regarding connecting rod modal analysis in ANSYS, it shows 6 different modes at result. i dont know what is that ? in static structural analysis if we apply a load to connecting rod its shows von mises stress in result , if von mises exceeds the yeild stress of a metal then we can conform it gonna fail. like this in modal analysis it is possible compare answer results in ansys software with theoretical result ? if so please reply?
Hi
Thanks for the article.
I have a general query.
By default the modal analysis is just for linear systems. So how could one find the natural frequencies of nonlinear systems (for example s structure with nonlinear boundary conditions) by the tools of a FEA software?
Regards
Thanks sir your all lecturers are very much useful for us.
Very nice article for beginners to understand the general followed process in design department for automobile products.
Cyprein,
I’m trying to follow your tutorial and have a problem in setting output results.
In Output definition Card when choosing Results>>Results there is a and I can’t specify anywhere this object so i can’t finish analysis properly.
Do You have any idea where the problem could be?
Not sure I understand your question. Is your problem to view the results in Paravis because they do not appear? Or is it something else?
Preparing analaysis in Salome-Meca I don’t have CALC_MODES in “Result” check box to choose (in your video: https://www.youtube.com/watch?time_continue=4&v=5SYHxrAr4f8
moment 22:26)
I think this is the cause I can’t carry out analysis properly.
If you don’t see CALC_MODES in here, I think it’s here because you didn’t define properly your ASSEMBLAGE or your CALC_MODES commands…
Can you export your .comm file and post if here? (just paste the content)
Hi Cyprien,
I’ve recently had to deal with some FEA related stuff at work and I’m a lay man when it comes to it. The concept here was explained in a very simple and easy to understand manner even for someone like me.
So thanks a lot for this article!
Regards,
Anirudh
You’re welcome Anirudth, I am glad that it was useful to you and help you in your job! Thanks for reading the blog.
Article was good sir. Can you explain how ansys calculate the modal frequency with given input .
Hi sir,
I have started my career on modal analysis.
I understand the resonance procicples but the thing that confuses me is the input frequency.
What is the input frequency of loading?
Thanks in prior.
Hi Mani,
The input frequency is only required if you do a “frequency response analysis”, in which case you have a dynamic load with is a function of frequency so you have to give the software you use the value of your input load in function of frequency as well (IF your load depends on frequency of course… you can also a load which is constant in frequency domain)
If you are talking about modal analysis, the frequency input you need to give is different, it is just a “range” in which you tell the software you want to search frequencies. The software only does what you tell him… and frequency are infinite so you want to search for a specific “area of frequencies” in which you know you will find some natural modes.
Hi,
I wanted to know how to identify the local and the global modes from a modal analysis obtained over a range of frequencies.
I have done modal analysis of a structure with on boundary conditions , thus I get first 6 rigid body modes which have zero frequencies. Now starting from the 7th mode, the frequency rises.
I want to know how to locate the global mode shape starting from 7th frequency.
Hi Gopal, to identify the response of each mode and the exact displacement induced by them, you have to constraint and load you model with a frequency dependent load and then do a “frequency response analysis” (make only sure that the range of frequencies you will sweep will contain the modal frequencies you are interested to see). I have another post on the blog explaining in details about frequency response analysis, check it out here.
Nice Explanation !!!!
Thank you, that really helps a lot.
Hi Rusu!
Im working with midasnfx and i have a question about one type of analysis case.
I already did a “Linear Static”, “Modal” and “Response spectrum” analysis and now im wondering if its possible to define a case with RS + Static Load?
I saw your video about “Modal Frequency Response” where you combine the modal+static but I want to use Response Spectrum + vertical Loads
Also is it possible create an acceleration/time function for define a new RS?
I really hope you can help me on this >_<
Thanks
Hi Grace,
I am not really sure about what you want to do here… are you trying to apply a static load and trying to get simulate it dynamically by adding a tie function? (In which case you should use a transient response analysis) or do you want to combine separately the results of a RS analysis AND the results of a linear static analysis? (In that case, you can calculate both separately and then add the displacements in the post-processing stage because both analysis are linear. There is function for that in the post-process). Adding a static load in a RS analysis doesn’t make sense for me as the Response spectrum analysis is a dynamic analysis… or are you talking about pre-stressing a structure before doing the RS analysis (there’s probably a way to do that too)?
Sorry for the confusion, I hope my answer gives you at least some orientation to try to solve your problem.
Cyprien
Hi! I wanted to combine my static results with RS ones, finally I found the way in the post process (Result combination panel)
Btw when you apply the RS but not considering the vertical loads that make your structure less rigid, thats why I wanted to add the loads.
Thanks ;)
Thank you so much for your great article. I need a little explanation on Global and local mode shape. What factor does influence the mode shape? In my analysis of complex structure in one direction, the global mode having high and local is low but the other side is reversed.
Very nice Article but I have one question Left.
Imagine i have a bar, which is clamped in on one side..
Now i calculate his frequeny for a longitudinal swinging.. In the nex step i wanna put a pressure on the free tip of the bar, the bar get shortened and the frequency of the longitudinal wave should get higher, so how would you calculate that?
That’s a very good question. You can do such simulation by considering the pressure like some sort of pre-tension. There are ways to couple a pre-tension analysis with a modal analysis.
Indeed ! Its a wonderful work for us beginners.
But I would ask a little stupid question , what are these modes?
Please , clarify it in the simplest of your terms that you are best at , Sir!
Further I would be pleased if you write an elaborated article regarding modes , mode shapes and all these mode including stuffs.
They confuse me a lot.
Mode ! Mode! Mode!
Please be simple.
Assume I am a dumb!
Thank You Sir.
A mode is a certain shape in which the model deforms at a certain natural frequency. For example, if your model has 3 natural frequencies 20Hz, 40Hz and 60Hz it vibrates in a different way at each of those frequencies. If you excite it at 20Hz with a load that excites the natural frequency, model will start to vibrate and take the deformed shape of the corresponding “20Hz Mode”.
Thank you Sir !
Now , I got it.
Can you please write an article about Harmonic Response Analysis and also random vibration analysis in ANSYS?
or just briefly describe the both.
Please !!
Thank you !!
Thanks for the explanation.
So in this case is local modes crucial or we do not consider them in analysis? For example of a constrainted structure, I have a target frequency of <35Hz, from simulation I obtained 1st local mode at 11Hz and 1st Global mode at 36Hz. Even though I met the target with the global mode, do I need to improve the local mode?
I guess it depends if your local mode vibrates with the same orientation than your loading or not and if yes, how much it vibrates. If your main dynamic loading condition only excites the global mode but not the local mode (for example, if you have a load always oriented in X direction, but local mode can only be excited by a load oriented in Y direction, it will never be excited, right?).
Frequency output in a mechanical system , where I ran modal analysis is 8 rigid modes and in mode 2 frequency is zero ,what’s the reason for 0 Hz and 8 rigid body modes.
When you get rigid modes, It means your model is not well constrained in one direction.
does changing the mesh size change the natural frequency obtained as output from the modal analysis?
Hi!
I want to perform a history analysis in nfx, but I’m not sure about the correct procedure in nfx: first, I created a time function where I upload my accelerogram data. Then I applied a dynamic load (acceleration) in the direction I’m interested in using the function create before, now I don’t know what type of solution type, I should consider ”direct transient response” or ”modal direct transient”
Can you help me with this? Is it correct the procedure?
Thanks for your interesting explanation,
I have a question about modal analysis. I modal analysis we can do analysis of a structure in mode free-free and clamped-free. I want to know the difference between those types and where we can use them.
Thanks a lot..
hello Cyprien,
Thanks for the article it helped me lot to know more about FEA.
My question is, for the simple analysis as you explained in video, why we get the 10 modes of natural frequencies ???
As you said if we avoid the system from Resonance i,e lesser than natural frequency(1st mode) then the system is Safe.Now, what’s the importance of the reaming modes in the list you show above.
i am little confused about this when we made the system safe(below natural frequency) but why the analysis tool showing the other modes also…..
please clarify me on this.
Modal analysis indicated all the possible vibrations modes of your system, but it doesn’t mean that all those modes are important. You have have to understand which of those modes are really excited under normal operation conditions. Suppose that your system has Mode 1, 2 3 and 4. Mode 1 and 3 appear only for a load vibrating in X direction in a certain frequency range. Mode 2 and 4 appear only for a load vibrating in Y direction in a another certain frequency range. Now look at your operation conditions and if the only possible vibration is a vibration in X direction, you can already eliminate Mode 2 and 4. Now check the operation frequency range and check if one of the Mode 1 or 3 can appear in this range. If no, you are safe, if yes, then you should find a way to move the dangerous mode in a frequency which is not dangerous. Makes sense?
Thanks for your efforts while writing the article first. I enjoyed reading it and I found out many things. My question is actually about the natural frequency of the structure. I know that the natural frequency is related to stiffness and mass. When I change the mass of the structure, let us say I made an optimization on mass and I have decreased it. What should I expect in the natural frequency of the structure? According to theory, I am expecting that the natural frequency of the structure increase. Am I right? but when I made a modal analysis on basic plate geometry, I see some of the mode increase and some of modes decrease? What is the main reason that I missed in this result? Normally, all modes should increase. My last question is about the force applying in modal analysis. In some of the modal analysis, the force is being applied as pre-tension. I realized that it is possible to get 2 different modes results in both cases. but we know from theory that forces should not affect the natural frequency of the structure. Why we get different frequency results in both cases? When should I consider the force as pre-tension in a modal analysis?
Thanks in advance for your assessments.
Best regards,
Emre
Your comment is awaiting moderation.
Hey Cyprein,
How you doing?
So as in your video, where you doing the Modal Analysis in the software.
How do you know if resonance has occurred? Which value you are trying to see if it matched with any of the frequency value being calculated in different modes? As you said resonance occurs when system (Plate here) frequency matches with the Load frequency. Right? Am I missing something?
Also,What are those red percentage sign mean? Does it indicate how close you are to resonance of something?
Will greatly Appreciate your response.
Modal only tells you the list of all possible resonance natural frequencies.
In fact, you can’t apply a load in modal analysis. You can only fix your model.
To know if resonance really appears, you have to apply a load and study the response.
To do that, you need to perform a frequency response analysis.
Note that if your load is dependant of time instead of frequency, you can also do a time response analysis and then use the FFT (Fast Fourier Transform) to calculate the resonance frequencies from the time signal you get in output.
Modal analysis can have loads applied. Lookup prestress modal analysis. Think about a guitar string, as you tighten the pitch (natural frequency) increases. Similarly a object that is spinning will be under load and its nat freq will also increase. This process can be accomplished in almost every FEM software.
Hello Sir,
I have been following your articles and tutorials. They are very informative and I like to read about FEA Analysis.
Sir, I have a question/doubt to ask for the modal analysis of structure.
In Modal Analysis, how to recognise the natural/resonant/critical frequency and corresponding mode shape in the model? Is it the first six modes or seventh mode is the critical frequency in free-free analysis. I always get confused about to chose the critical frequency.
It will be very helpful if you can explain me.
Thanks,
Anup
Your explanation is just too clear and simple.. Thanks a lot..
thank you so much for such a beautiful article.
my question is,
how to decide the number of modes to be extracted while performing a natural modal analysis?
Hi,
can you explain me about relation with eigen value and frequency ?
can we solve the component without constraint ?
Hello @Cyprien
Thank you for you valuable knowledge and efforts to enlighten others.
Thanks, others also for their valuable comments.
I am working on some projects Modal and response analysis.
We mostly knew that Natural frequency should be less than the Operating frequency.
Is there any criteria/method to decide, what or how much value natural frequency deviates from operating frequency to avoid resonance.
Regards
Manav22
First of all thanks a lot.
I have a question, In ultrasonic assisted machining, ultrasonic welding etc. systems, transducers are required to vibrate in eigenfrequency . If we vibrate a system at its natural frequency ( eigenfrequency ), won’t there be resonance? Why do we want to vibrate in mode shapes ( eigenfrequency )?
Thank you very much. I understand the meaning of modal analysis . Best regard to you
Hi Cyprien,
Modal analysis has to be carried out only if we intend to run dynamic analysis, is that correct?
If we only intend to only carry out static analysis for certain type of structure, we can basically ignore modal analysis.
Yes, that’s correct. If your analysis is always static and you are not interested into studying the vibrations due to dynamic loading, then you won’t need to perform a modal analysis.
Thank you for your detailed explanations.
Thank u sir😭,helped me a lot to prepare for the viva,i am still an undergraduate and i had no idea about it.
It was helpful when you explained that static analyses vary from dynamic ones in that they don’t depend on time. My brother is interested in working with FEA services to optimize the construction business he’s planning on opening around next spring. Asking about static and dynamic analyses should help him find a knowledgeable FEA service, so thanks for sharing that idea I can pass along to him!
The collapse of Tacoma Narrows bridge is often attributed to resonance. This is not correct. The collapse is due to galloping, which a self-excited vibration phenomenon.
I thought I would let you know.
Can you explain this phenomenon? Thanks
Hello, great text!
If I run a modal analysis with a support condition and ask for only 1 mode and run another with any kind of support and ask for the 7th mode, will the result be the same?
I mean, the only difference between with and without a boundary condition is that without I will have the rigid body frequencies?
Thanks for the attention!
I am new to FEA however not new to Simulation-Based Product Development
This blog & associated Youtube channel is the best place to clear your doubts
Thanks, Cyprien Rusu for your continuous efforts to spread the knowledge
Why ‘rigid body’ modes have natural frequency equal to zero? For first 6 modes, unconstrained solid body acts as a rigid body, i.e. body stiffness, k = infinity, in that case natural frequency should be infinite as per the definition of natural frequency [wn=(k/m)^1/2], then why in modal analysis we get zero value for natural frequency of these modes?
thank you so much for the clear explanation.
I say big thank you for the basic as well as practical knowledge you have given. I hope I further study and implement them in practical industry works.
I am comparing 2 models for their natural frequencies.
1) First I am performing Modal analysis without any constraint for both models.
Model 1 is giving higher frequencies at respective mode shapes.
2.)But, after giving same constraint to both models, Model 2 is giving higher frequencies at respective mode shapes.
Can you explain if this is possible & how? Thanks in advance!