Today, I am sharing another article written by Nick Ananchenko, an Ukrainian Mechanical Engineer expert in Code_Aster
You can check his previous article here:
Engineer Story: Why should you develop your own Code_Aster Module?

Hello everyone, my name is Nick Ananchenko, and I am mechanical engineer, with great passion for my profession. I used to work in Paton Electric Welding Institute, Kiev, Ukraine where I learned how to use FEA packages. I have been involved with research work, along with some projects for Ukrainian nuclear industry. I also did an internship in Concepts NREC, a worldwide leading company in turbomachinery software, as a software engineer, where I learned a lot about software development.
Check Nick’s Linkedin profile here
You can also contact him by email: Nikita_Ananchenko@i.ua
- Is free software as efficient as a commercial one?
- Can Code_Aster replace Abaqus or other commercial software?
- What is the accuracy of FEA analysis?
- Can engineers mistakenly obtain results which are very different from the reality?
Read the answers to those questions and more in this article.
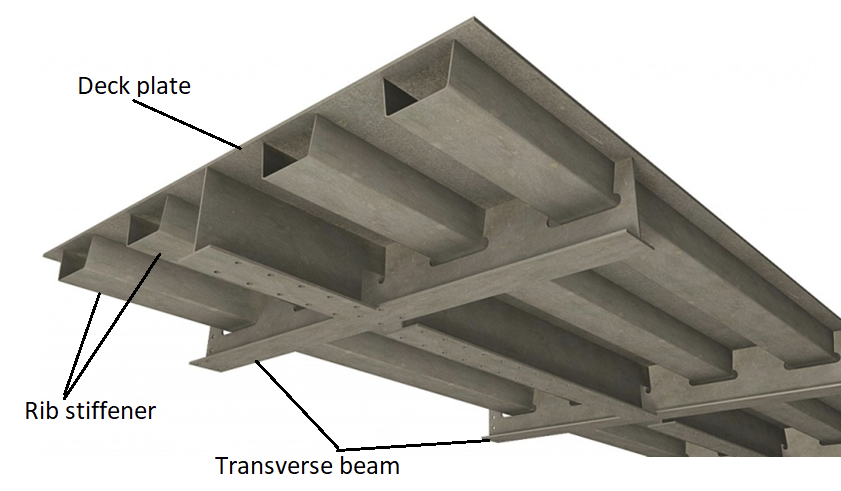
In my latest project I’ve used both Code_Aster and Abaqus Learning Edition in order to compare usability of these softwares, and to see the difference between the two obtained solutions. As a part of larger project, bridge orthotropic deck stress analysis was made in order to calculate its deflection.
The problem of large deck deflections affected in a cracking of the bridge’s asphalt surface layer which results in costly annual repairs. In order to get rid of the large deflections, strengthening repair of the bridge deck was designed by adding reinforcing plate to the orthotropic deck plate, as we will see below.
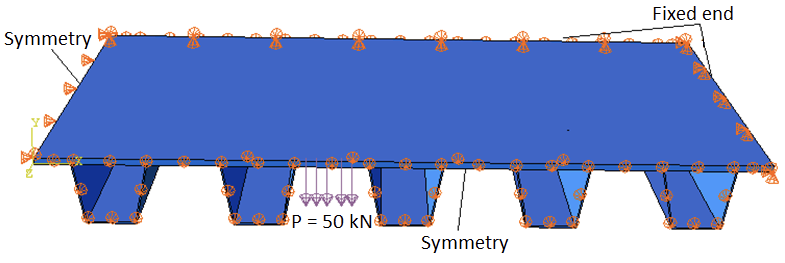
Orthotropic deck FEA model was created in both Code_Aster and Abaqus. Section between two longitudinal main beams and two transverse beams was analyzed, load from the car wheel (50 kN) was applied between two rib stiffeners to obtain a maximum value of out-of-plane deck deflection. For saving the computational recourses and in order to build a fine mesh, a quarter of the section was considered, thus two ends of model were applied with symmetrical boundary conditions, and two others are fixed.
FEA analysis was made and stresses with displacements were calculated. But due to the local nature of loading, deflection and stresses occurs only at the local area of applied load, where finite element method cannot guarantee an exact solution. Optimization of FEA analysis is required to achieve one.
The first variable to improve is the number of elements throughout the thickness of the plate and the second one is the shape function of the finite elements used.
General approach for thin plates under transverse loading require at least three elements throughout the thickness, and while increasing the number of elements throughout the thickness, the solution (stresses, displacements) should converge to almost a constant value.
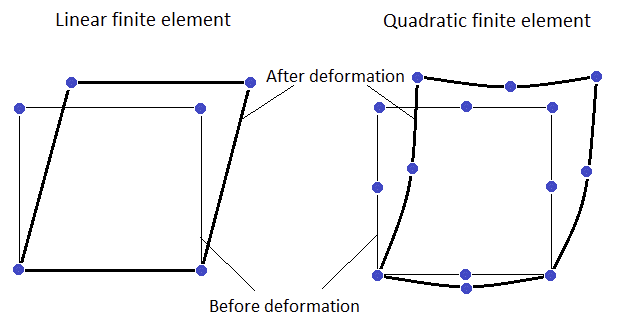
Other important thing is the degree of the element’s shape function used: linear or quadratic.
What is the difference between linear and quadratic finite elements?
Quadratic ones have an additional node on the edge, compared to linear, which means that quadratic element comply with the second order equation (ax2+bx+c) while linear comply with the first order (kx+b).
That allows quadratic elements to experience bending, while linear cannot experience it.
As the FEA model was made in both Code_Aster and Abaqus I need to say that the major difference between two softwares is the mesh generator.
Code_Aster (Salome Meca) does not have a wide range of automated mesh generating algorithms, therefore I’ve had to use GMSH to build a mesh and then export it to Code_Aster.
While Abaqus has very straightforward and intuitive mesh generating algorithm that requires very small amount of time to built a fine mesh. I should note that I get used to Abaqus mesher, so I can be biased here.
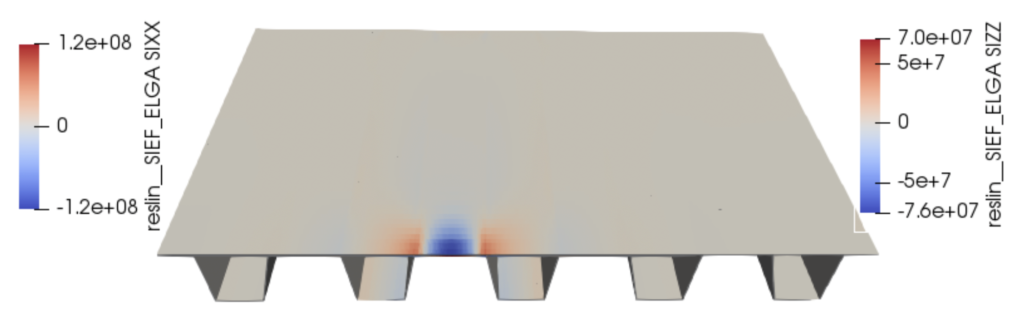
Deck out-of-plane deflection was calculated, as well as equivalent von Mises stresses along with all stress components. As we can see below, solution obtained with Code_Aster with three elements throughout the thickness and a quadratic type of finite element shows that maximum deflections (1.2 mm) and equivalent stresses (110 MPa) indeed occurs in the local area of applied load, as well as transverse (+119/-119 MPa) and longitudinal (+70/-76 MPa) stresses.
At the upper surface where the load is applied, transverse and longitudinal stresses are compressive, at the lower surface stresses are tensile. Unlike maximum compressive through-thickness stresses, that occurs in the walls of rib stiffeners.



Solutions obtained by Code_Aster and Abaqus were compared for one, two and three number of elements throughout the thickness and for linear vs quadratic types of finite elements.
Type of finite element plays crucial role in the accuracy of solution, at this particular FEA analysis, due to a local bending of the plate.
Linear finite element usage has led to unrealistic results, as obtained this way stresses and deflections are three times lower from the real ones.
Also, while increasing the number of elements throughout the thickness, stresses in Code_Aster has converged with up to 5% accuracy, which is sufficient. In Abaqus, the solution has converged (up to 1%), regardless of the number of elements throughout the thickness.
Nevertheless, solution for three elements throughout the thickness and a quadratic type of finite elements did not completely converged for Code_Aster and Abaqus, giving 4% difference in obtained deflection, and 8% difference in obtained stresses.
Also, direct method of solving the governing equations was compared to an iterative. Direct method means that FEM equation in a matrix form {F} = [K]{U} solved directly, while iterative means that equation {F} = [K]{U} solved iteratively, and gives an approximate solution. For both Abaqus and Code_Aster direct and iterative methods gave the same results, with less than 1% difference.
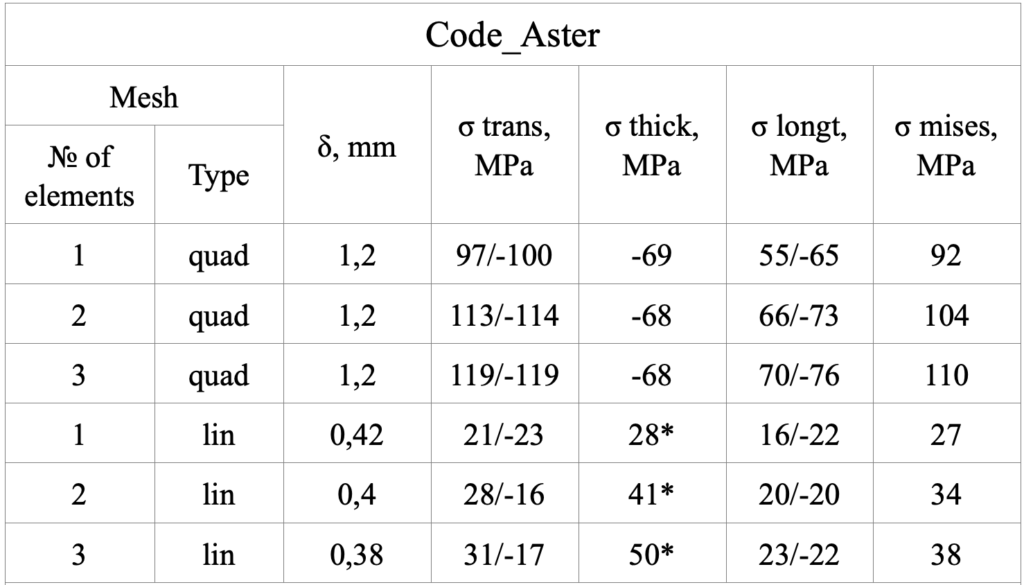
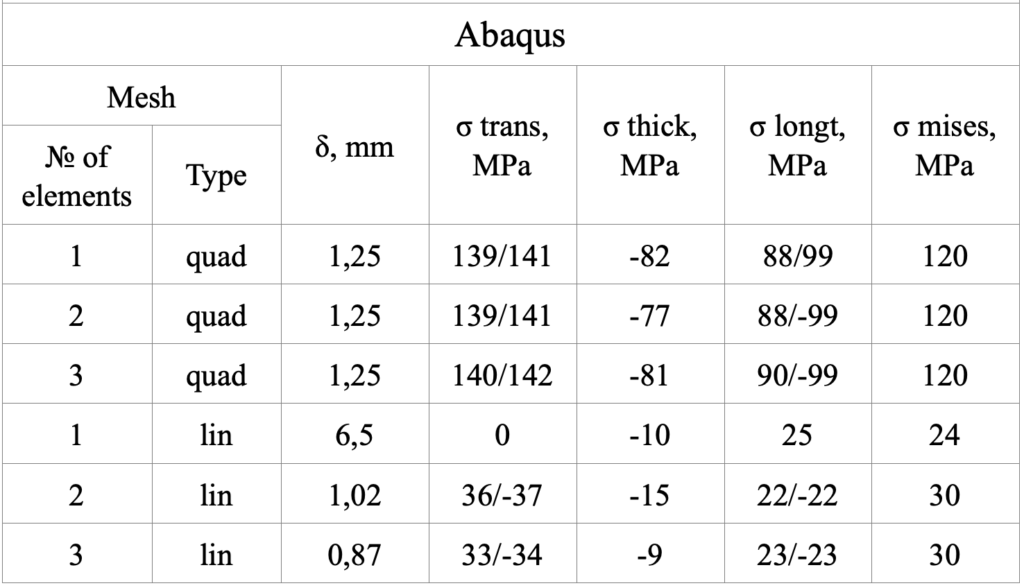
*starred stresses occurred at the deck plate in the area of applied load, due to inaccuracy of the solution for linear type of finite elements
In order to prevent a cracking of asphalt surface layer, reinforcing plate was added to the orthotropic deck plate. Two options of welding repair were considered: with whole welding of 16 mm reinforcing plate to 10 mm deck plate, and with gaps in the welded 16 mm reinforcing plate to 10 mm deck plate.
As it can be seen below in the figures and in the table, first option of whole welding of reinforcing plate to deck plate is a better choice for the strengthening repair.
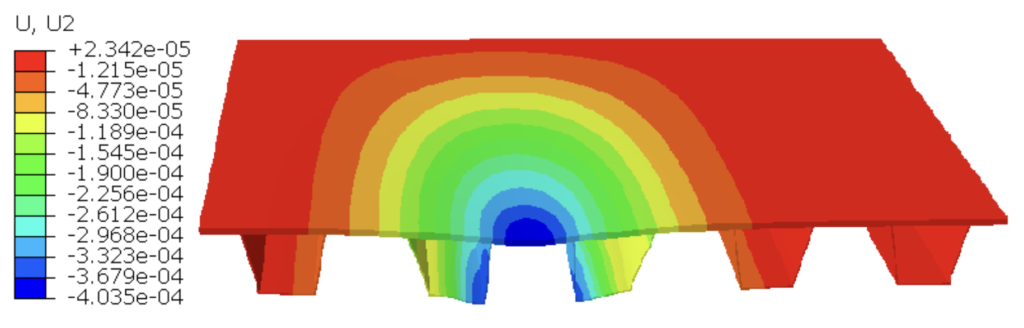
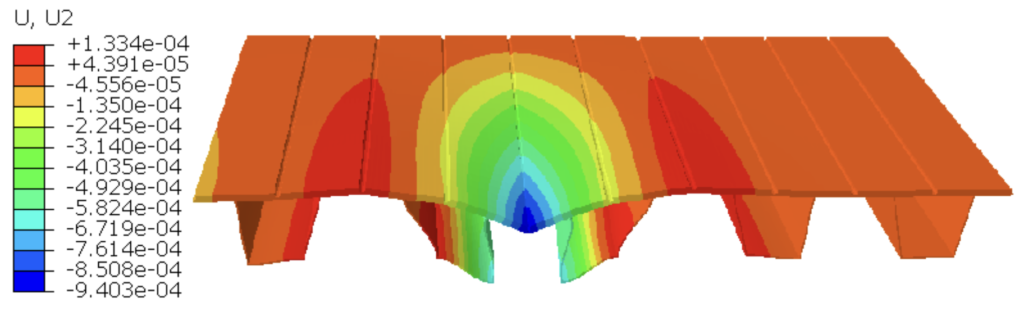

Conclusions:
- Type of finite element (linear or quadratic) plays crucial role for thick walled structures, or for structures that experience bending
- It is recommended to use at least three elements throughout the thickness for thin plates. While increasing a number of elements throughout the thickness, solution should converge
- Direct method of solving the governing equations did not played a crucial role, in this particular analysis, in comparison to an iterative one
Special thanks to Jacques Berthellemy from Cerema for sharing his wide experience of bridge design and maintenance with me.
– Nick Ananchenko
You can download the Code_Aster HDF files and mesh of this model here:
https://github.com/CyprienRusu/Feaforall/tree/master/Salome%20Meca%20Tutorials/Bridge%20Deck
Models named Meshi, where i- number of elements throughout the thickness, letter ‘a’ at the end – for linear element type.
If you have questions for Nick, please don’t hesitate to contact him at his email address: Nikita_Ananchenko@i.ua

You can also leave comments on the blog article as usual and let me know what are your thoughts or your experience in this area!
Cyprien “Really hoping Ukraine will go better soon” Rusu
Nice article.
Thanks a lot
It’s a pity that he didn’t use shell elements in both cases. There might be less difference in results. There’s also no information about quality of the mesh. This also plays a significant role in obtaining better accuracy. He might also use the same mesh in both cases.
As for the results, we always assume that commercial software is “right” and the open source should replicate that result. Abaqus, Ansys etc. have their own bugs so bug fixes are provided due to paid subscription or etc. I tend to be very cautious making strong statements, so I will only say that no one should say that Code_Aster is less accurate…