It’s been a long time since the last time I wrote on the blog, but FEA is an area where there are a lot of things to explain and I will continue to explain the contents which interest most of FEA engineers.
Thanks to Fisible for proposing today’s subject ;-) I am waiting for your feedback in the comments…
So, let’s begin the topic by some elementary notions… what is an FEA solver ?
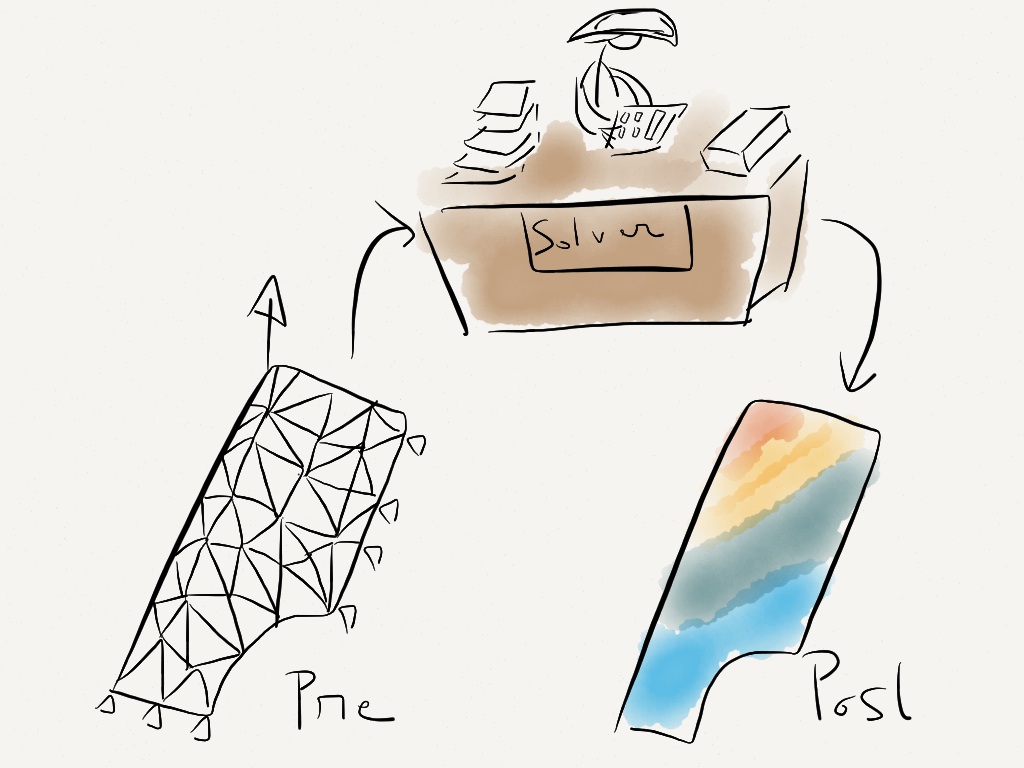
Well, basically, every FEA software is composed of 3 parts the Pre, the Post and the solver. As the pre and the post can be found through the user interface, we understand generally easily what it represents, but the solver remains a bit mysterious…hidden behind the interface to solve all the problems ;-)
The job of the PRE (process) is to create the model, the preparation of the geometry, of the mesh, the definition of the properties, the materials, the loads and the boundary conditions.
Then, a text file which includes all these data under a specific standard format (generally Nastran) is generated and send to the solver.
The job of the solver is to take these input data, to process them using specific algorithms (I will detail that a bit later) and to give an output that correspond to the result of the analysis.
These data are then sent back to the POST (process) which will “open the package” and display the data in a form that will be understandable for the user (contours, graphs, tables,…).
So in fact the solver is kind of the “Brain” of the software. It contains all the algorithms that will be able to decompose and process the input data to get the results needed.
Ok this is nice to explain all that….but how does it work ?
Here finally comes an interesting question ;-)
Let me explain how it works in midas NFX !
A system of equation solver is used not only for linear static structural analysis, but also for all other types of analyses such as eigenvalue, buckling, dynamic and nonlinear analyses.
Generally, two types of solvers exist: a direct solver, which is based on the Gauss elimination or LU decomposition; and an iterative solver in which errors are minimized and solutions are converged through iterative calculations.
A direct solver is widely used in structural analysis because finding solutions is stable without being affected by the numerical characteristics of the matrix. But it rapidly tends to demand a significant memory space and a large amount of calculations for a large problem in which case an iterative solver requiring relatively less memory is more desirable.
For structural analysis, however, it must be cautioned that an iterative solver may not provide the desired solutions due to the numerical characteristics of the matrix, or the amount of iterative calculations may become significant in arriving at converged solutions. midas NFX provides a function that automatically selects between the direct solver and iterative solver depending on the scale of the problem required to be analyzed.
A direct solver obtains the solutions to a system of equations in two steps. The first step involves matrix decomposition, and the second step pertains to the forward-backward substitution (FBS) process. The LU decomposition method, which is applied to a general asymmetrical matrix, can be applied to decompose a matrix in the following form in the case of symmetrical stiffness matrix, K , generated in the process of finite element analysis.
The important aspect of using a direct solver is to properly use the sparsity of a matrix. Generally, the stiffness matrix, K , generated in the process of finite element analysis is a sparse matrix containing numerous 0 terms, and the amount of calculations and required memory space significantly change depending on the method of utilizing the sparsity. midas NFX supports a dense solver for solving a general dense matrix, which does not utilize the sparsity of the matrix. In addition, midas NFX supports a multi-frontal solver as the basic direct solver, which can remarkably reduce the amount of calculations and memory space while appropriately utilizing the sparsity of the matrix.
The multi-frontal solver orders the degrees of freedom to minimize the amount of calculations and memory space utilizing the sparsity of the matrix. The matrix is then divided into a number of frontal matrices based on the ordering data, which are subsequently decomposed. The algorithm of recursive bisection is used to implement the ordering of the degrees of freedom. The forward substitution takes place in the same order as the matrix decomposition while the backward substitution is calculated in the reverse order.
An iterative solver uses a method, which reduces errors in approximate solutions obtained through an iterative process leading to convergence. It is crucial to rapidly reduce the convergence errors in a small number of iterations. Generally, the number of iterative calculations depends on the preconditioning technique. midas NFX uses the SA (smoothed aggregation) AMG (algebraic multi-grid) method, which is known as a stable preconditioning technique, irrespective of element shapes.The AMG method uses multi-grids so the number of iterations is not greatly influenced by the number of degrees of freedom. It also exhibits stable convergence when using elements consisted of displacement and rotational degrees of freedom at each node such as shell elements. The iterative solver using the AMG method automatically composes multi-grids, which are created by the sets of neighboring nodes and the degrees of freedom representing each set of nodes.
As explained earlier, the performance of a direct solver or an iterative solver changes with the scale of the problem to be analyzed for which midas NFX provides a function making an automatic selection between the two. When the function of automatic selection of an equation solver is opted, an appropriate solver is used on the basis of the problem size. The direct solver using the dense matrix is selected for a small scale problem. The multi-frontal solver is selected for a mid-scale problem. And the AMG iterative solver is selected for a large scale problem. The criteria for automatic selection are determined by considering the following aspects:
► If the empirical condition is known: determined on the basis of the nodes or the number of elements specified by the user
► If the empirical condition is unknown: determined by the program based on the number of degrees of freedom of the model and the system memory size
There is still a lot more to explain but it will be for another article ;-)
I hope the FEA solver is not anymore a mystery for you !
Let me know your comments about this article by leaving a message in the comments :)
Hi Cyprien!! congratulations for your post.
I have some comments about this affirmation ” The multi-frontal solver is selected for a mid-scale problem and the AMG iterative solver is selected for a large scale problem. The criteria for automatic selection are determined… ” I am sure that in many cases the automatic option is much better than anything else, especially for inexperienced users, but perhaps would be good to change the convergence tolerance of the iterative problem, that could take too time to converging the solution.
Thank you very much for sharing your knowledge about NFX . ;-)
Hi fisible, nice to see that you read my article ;-)
I agree with you too about the convergence tolerance and of course you can set this tolerance ;-) You have actually 3 types of different tolerances: in displacement, in load and in work. You have also to possibility to choose manually the options for the method used for the convergence (Full Newton Raphson, modified Newton raphson, …) and also some specific methods like the Arc length method for specific case (Nonlinear Buckling).
Is perfect friend, I think that this program continues to be live up to this competitors, which pleased me… I speak from the little I know of this software… I think it’s a great FEA tool.
I believe that new version are very promising. We hope your comments too.
Thank you very much for sharing your time with us.
:-)
Very helpful post. You just clear many things through words, rather than equations..
Thank You Biki, I am glad that it helped you to understand better the topic !
Hey,
First of all, a very good post. I am a novice FEA engineer. I had not yet found an article that explained direct and iterative solvers so well in words. It has given me a lot of clarity. But I am very confused as to what happens during meshing (mathematically), apart from breaking the geometry into smaller domains. Stiffness matrix is for a particular type of element. So all the stiffness matrix together form the final matrix for LU decomposition? Also, what equations does the solver use after the LU decomposition to reach the final solution?
I have done my research but I am thoroughly confused and I can’t seem to find the right answers, nor put my thoughts in a line.
Thanks for the help.
Very good comment Aalekh and I have to say that if you really want to enter in the profound details on how the decomposition works you’ll have to take a look on the mathematics of finite elements. There are a lot of good books on the topic like this one for example: http://www.amazon.com/Mathematical-Element-Methods-Applied-Mathematics/dp/1441926119/ref=sr_1_6?ie=UTF8&qid=1427974996&sr=8-6&keywords=finite+element+theory
But I guess you will only need to know that if you plan to develop your own finite element software…is it what you are interested to do?
Not exactly. Actually, I just have this need to know because I cant wrap my head around it. As I stated earlier, I have all these ideas but I can’t seem to put them in an order which make sense.
Very useful posts cyprien. It cleared the doubts regarding solvers. Please post more Posts, it is very helpful for me.
THANK YOU! :)
Thanks for the post. It was always a mystery to me as to what is a solver.
Thank you, Cyprien!
Although I didn’t get a good idea about the solver among which one is better, either direct or iterative method. But I think it is my fault to not understand well. You know why I am not clear still because I studied somewhere else that iterative method is good if compare to direct because of taking low memory and less time but here your article makes my head twist around huh!
Could you please brief me that what are the major differences amonge.