In this article, I will tell you the very basics you need to understand to start using nonlinear material models in your FEA simulation.
If you are just starting FEA, you may have learned that defining “Material Data” usually meant providing 2 input values into your FEA software:
- The Young’s Modulus
- The poisson’s ratio
And maybe other additional parameters such as the density of the material or the thermal expansion coefficient…
Why can you define your material with so few data?
That’s probably the first question you should ask yourself…
And the obvious answer is:
… You can’t ;-)
Well… at least without a lot of simplifications.
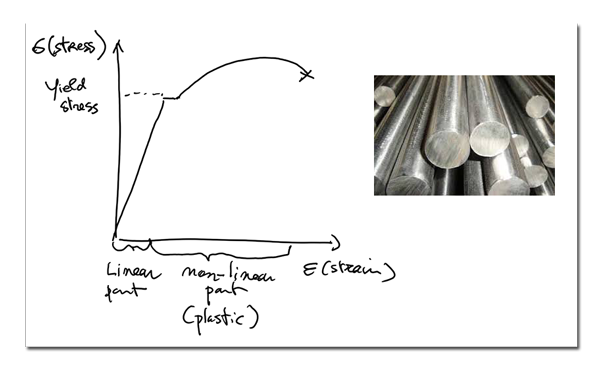
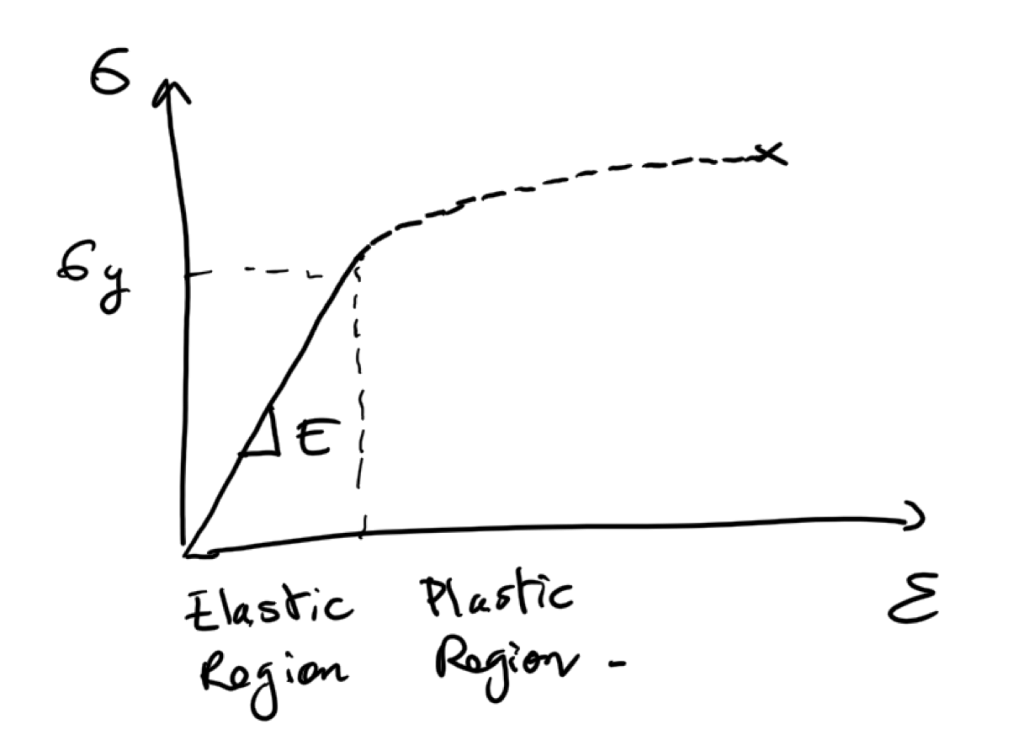
The usual material used in mechanical engineering is steel and we mostly define its characteristics using a very important curve called the “Stress-strain curve”.
Like this one:
This curve is obtained by doing testing in laboratory on small samples.
The linear material assumption
In most cases, the FEA analysis designers perform to test simply their design is a linear static analysis which ALWAYS takes as an assumption very small deformations of your material.
(You’ll have more details about linear static inside the free course here)
So… to be short and straight to the point, in linear static analysis, the material used is always also considered as a linear material.
What does it mean?
it means that we are only considering the very left portion of the stress-strain curve and we consider it to be a straight line.
That’s an assumption valid only for very small deformations (strain), of course…
How do we tell the FEA software what kind of line our material has?
We use the Young’s modulus for that.
The most basic definition of the young’s modulus is that it’s a coeffticient which represents the slope of this initial straight line.
We call this kind of material an “Elastic Material” because it behaves elastically like a spring…
You give it a certain load and the material will deform and extend (or contract) in the same proportion (that’s why it’s called a “linear” relation)
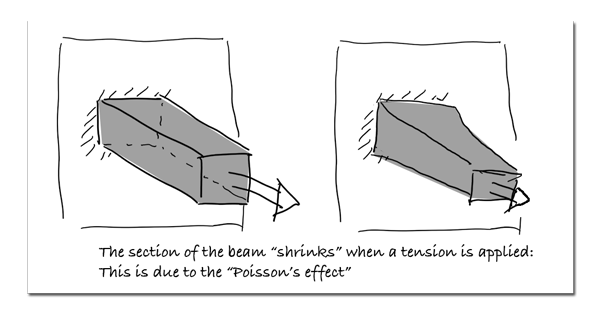
Now, a quick word about the second parameter… the poisson’s ratio.
When a load is applied to a beam and the beam extends for example, the section also decreases (because the volume stays the same, right?)
This effect is represented by the poisson’s ratio.
The astonishing thing is that we just need those 2 parameters and that’s all!
If you consider also the gravity, you will need to have the mass too, and then you need to add the density of the material (to calculate the mass)
Now, what if I want to study a material which deforms A LOT?
That’s when the hypothesis of small deformations we did previously doesn’t work anymore…
Typical examples would be:
- We are studying a material closed to failure
- We are studying plasticity (constant deformation)
- Our material simply doesn’t have this kind of linear range
- Etc…
In one of those cases, we have to find something better to represent your material…
And unfortunately that means also we have to go one level upwards in term of difficulty, because we enter now in a much more complex domain…
The domain on “Nonlinear FEA Simulation”
What is a nonlinear material?
That’s where things become tricky because a non-linear material is just a material which is “NON – Linear”…
So, except knowing that the material curve is not a line, you still don’t know much.
In fact, there are plenty of non-linear material models out there that can be used.
A material in general is a very complex arrangement of mater
… and concrete material is VERY different from Soil material, which is also very different from plastic material…
That’s probably because the reality is much more complex than any model engineers can invent to try to match the behaviour of specific materials.
So you will find models for almost every type of material:
- Elasto-plastic material model
- Perfect plastic material model
- Visco-elastic material models
- Nonlinear elastic material model
- Hyper-elastic material models
- Loading History dependant material models
- …
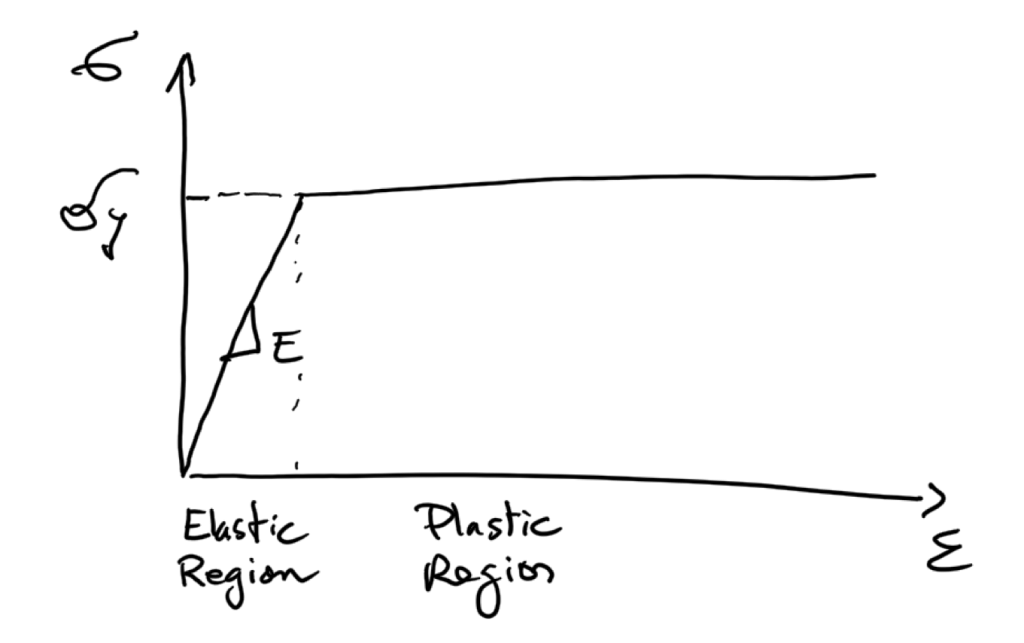
The tricky thing you should remember is that once you reached the yield strain/stress, you enter into the “plasticity” domain. As you are not in the elastic domain anymore, you won’t have a direct relation between stress and strain.
You rather are working with increments of strain/stress.
The total strain increment can be decomposed into elastic strain and plastic strain increments.
In elasto-plasticity, there something called a flow rule, which is the relation used in nonlinear material models to calculate increments of stress and strains.
Said simply, elastic material always comes back to initial shape after you remove the load because it’s elastic, but as soon as you get a deformation and your part becomes plastic somewhere, your part starts to change shape for good which induces problems when you unload and load it again…
You can imagine some kind of “yield surface” which will change shape either uniformly or in certain plastic areas only.
I won’t explain about all that here in details, that would be going a bit too far… maybe I’ll talk about it more in details in another article.
Now…
How to choose the right nonlinear material model?
This is a big topic and I will only give you some clues about the most important material models you should know about and you can choose the most appropriate to your simulation in function of the material you have and the simulation you do:
Perfect elasto-plastic material model
This is probably the simplest of all nonlinear material models. It considers that once the yield stress is reached, stress becomes constant and only strain continue to increase.
That’s a very big assumption and probably only valid for steel materials near the yield stress (in reality stress continue to increase a bit until the ultimate stress limit is reached)
It’s a very easy model to set-up (you only need the yield stress value…), but don’t overuse this model just because this is the only one you can easily setup as you don’t have the required stress-strain data… you would just get wrong results.
Multilinear hardening elasto-plastic material model
This model is an improvement of the previous model. Instead of considering the stress constant equal to the yield stress in the plastic region, plastic stresses are calculated using a “hardening” curve.
It is called “multi-linear” because the hardening part (the nonlinear part of the curve) is calculated using a series of points provided by the user (you) and then approximated with a linear approximation on each segment between the points.
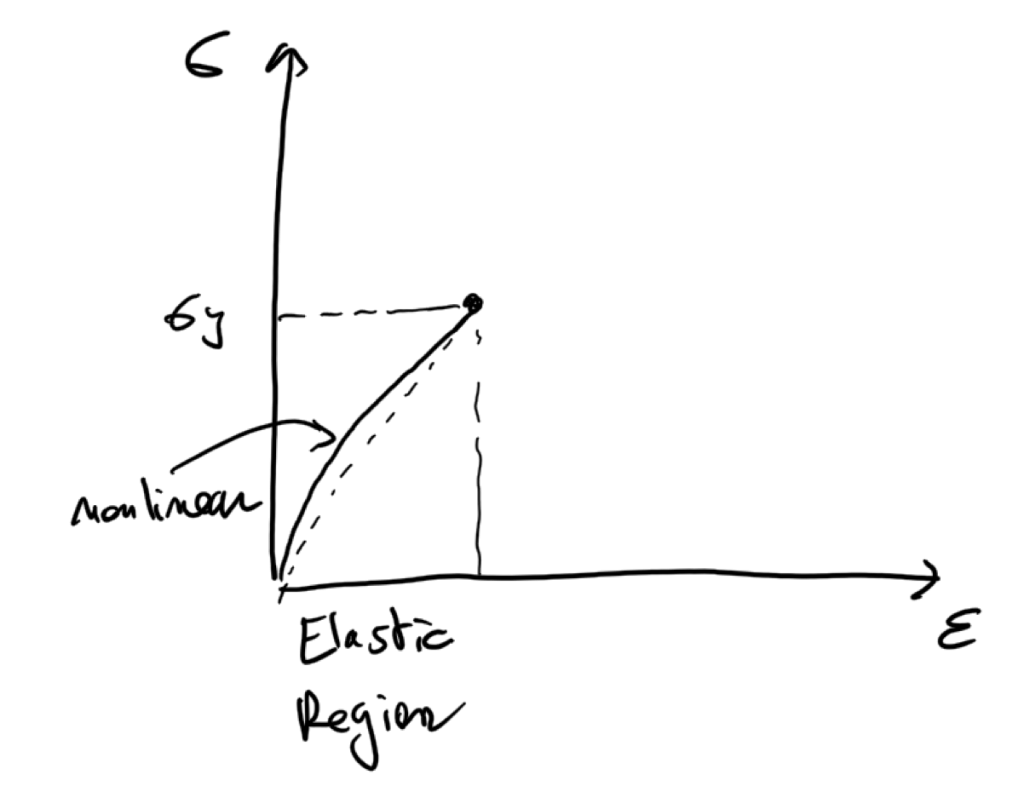
The nonlinear elastic material model
Some materials (especially plastics) tend to have an elastic region which is nonlinear in itself.
It means that if you applied a load with a value inferior to the yield stress and then you unload your model, the model will effectively come back to its original shape… but the stress and strain won’t follow a linear relation of proportionality.
There are much more to say, but again, I am just scratching the surface to give you an idea here.
As a side note, if you are a Salome-Meca user, you will be glad to know that it boasts to support more than 200 constitutive laws… with such awesomeness under the hood, you can hope to spend many glamorous days calculating stress in your idle time.
Now the big question:
How to define an Elasto-plastic Material?
I think you already guessed it…
The reason I talked about the “Stress-strain curve” in this whole article is because that’s the main data points we need to define a nonlinear elasto-plastic material into an FEA software.
How to get this “stress-strain” Curve?
Well, the bad news is that it comes usually from laboratory tests…
If you are using a steel material or another well-known material in engineering, chances are that you can easily find a corresponding stress-strain curve on internet for it.
(There are online material databases such as Matweb)
Such nonlinear material data is usually not provided inside the material library of existing FEA software because such data are very specific to your material.
(If FEA vendors provided nonlinear material curves inside their databases, everyone would use it wrongly and that would create a lot of mistakes… or at least much more than now)
Now if your material is non-standard, you will probably have to do some laboratory testings…
How to input this curve in your FEA software?
There are several ways to input this curve, depending on the software you use but all are pretty much similar.
You either directly input data points and the software does the job to interpolate job to reconstruct the curve.
Or… you have some kind of models implemented into your software which can help you to have a nonlinear material curve.
For example, the “perfect plastic model” is basically just a linear curve in addition with a constant portion that starts after the yield strength is reached…so it can be defined just with the yield stress value.
Also generally, in your FEA software, you will have 2 ways to input those data: Either by give it the full curve or by providing only the hardening curve. Be careful because the hardening curve doesn’t start at zero.
Ok…That’s all for today!
Other Article Related to Nonlinear FEA:
5 simple tips that will simplify your life in nonlinear FEA analysis
/////////////////////////////////////////////////////
You maybe noticed that I wrote a lot of great educational article… that’s because I really want to contribute and help engineers who are new to FEA to understand those concepts better and faster!
I am not hiding that it takes a lot of efforts to write all that, so…
If you like this article, there are 3 things you can do for me:
1- Help me to share this article on Linkedin, facebook, twitter or in your habitual forum to help more people understand Nonlinear material models (use the share button on the left of the article).
2- Let me know in the comments what you learned from it and what you would like to learn even further so I can write more on the topic
3- Join the newsletter (if you are not already subscribed), I’ll send you everything I write (and much more) by email!
Thank you for reading!
–Cyprien



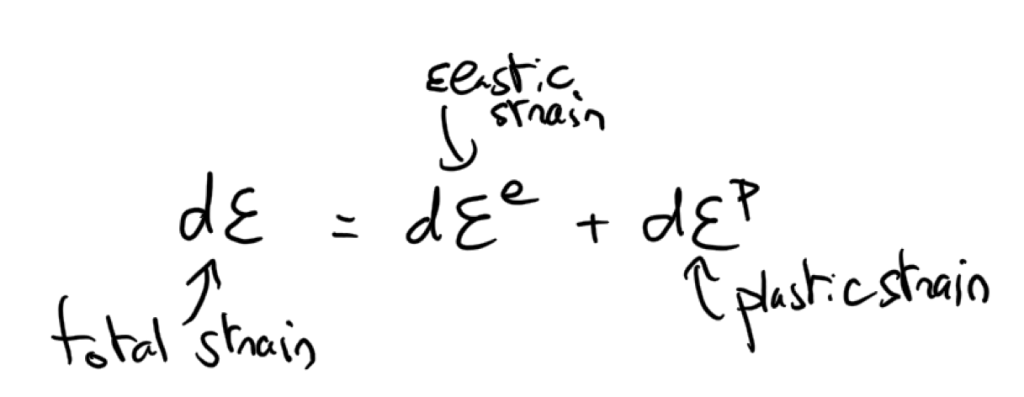



Nice! Let’s note that not only steel but lots of material can be simulated. For example I currently work on a visco-plastic model in order to simulate soil with high strain rate using the Perzyna model. I use an associated flow rule with a custom yield surface and hardening law. I that case results are highly dependent on strain rate.
Very interesting! I would be glad to know more about this “Perzina Model”!
Great article!! Actually I’m trying to simulate the tensile test of a polymer dogbone using the stress-strain curve of the material (ABS) as input, without success. The analysis doesn’t converge. I hope a second part of your article. I have a lot of questions about the differences between implicit and explict fem analysis, advantages and drawbacks, etc. And the relation between each scheme with nonlinear behaviour of the materiales, is there into your page any article about it?
Hi Luis, I have to say that this topic indeed deserves an article! From memory, this webinar in which I contributed by my friends Piotr Stephen and Renier J. Van Vuuren will give you some interesting clues, it’s worth watching: https://www.youtube.com/watch?v=P5DjkDA-_eg
Great article Cyprien. Thanks for posting. Educative and informative.
Regards
Shashi
Understanding Material properties extremely important in FEA. And I found most of FEA engineers make very less efforts to characterize their own materials. Typically non-linearity plays huge role in case of plastic and elastomers. Also we need to understand the way plastics are extruded or molded changes it’s critical material properties…Espicially in plastics there are many grades and better FEA engineers characterize it’s own materials keeping manufacturing flavour intact sothat when you characterize these materials in lab it will capture exactly similar properties.
Polymers like HDPE can be defined using below approx values..E = 1000 MPA.. Poisson ratio= 0.39…Yield stress= 25 MPA and tangent modulus approx 15 MPA (bilinear isotropic hardening)…
But above value will change once you will change your manufacturing process…similar for rubbers and other materials…
Another intresting area is contact and convergence handling with these type of nonlinear materials..
Pl reach me if someone have any queries related to materials and FEA at mittalmanoj2k@yahoo.com …I would be happy to discuss with you problems…
Hi I would like to ask you, it is there some example in AsterStudy, how to define non linear analysis.
Thanks. Vit.
Hi Vit,
You can check my latest video tutorial, it is a nonlinear static analysis with contact:
http://feaforall.com/nonlinear-hertz-contact-tutorial-salome-meca-2018/
Cyprien
Great article! I’d like to learn more, is there a follow-up article?
How would you setup an FEA for polycarbonate-urethane (PCU) material?
Maybe something similar to this:
https://www.dsm.com/markets/medical/en_US/products-page/products-biostable-polyurethanes/product-pu-bionate-pcu.html
This article was too indispensable for my simulation and finally, I got it. I would like to say thanks for such an informative and easily explained article.
I am wondering about one thing which I am facing difficulties about, Why people use true plastic strain rather there is not much difference between the true stain and plastic strain. If there is a difference so how it is?
You’re welcome Mubasher! From what I can remember now, true plastic strain is only the plastic part of the true strain (You have to add the contributions of elastic and plastic strains). If your purpose is to look at the plastic failure, you are probably more interested to know where the strain becomes plastic first, which is easier to see with true plastic strain.I hope it answers your question!
Very nice..!..thanks a lot
Greetings from Nepal!!!
very nice introductory explanation. thanks for writing such a short and comprehensive article. i would like to know about weighted residual methods, especially galerkins. i dont know how a differential equation is converted into an algebraic one based on variables at nodes. i would love to have an explanation on that from you.
but as an engineer, is it necessary or how much necessary that i know that process?
Hi Amrit, It’s always interesting to know the math behind behind FEA and the equations, but if you are an engineer, I would say that this is of secondary importance. Most of the important math formulas and equations are already coded into the FEA software that are used in each industry. In engineering, the most important is to understand in depth the system you are studying, its behavior and how to improve it! The math used is generally restricted to 1D or 2D formulas for simple verification. Anything more complex than that is done using a software. Now… it always depends! So if you like to learn about weighted residuals and Galerkin method, there are plenty of books available, go for it!
Hello Cyprien,
The article was quite informative, but I would like to have some more information on the choice of the Material Laws to be used to define an Elasto Plastic Material. The 4 Material Laws that I am aware of are:
1. Perfect Plasticity (corresponding to your Perfect elasto-plastic material model),
2. Linear Hardening Law,
3. Power Law, and
4. Exponential Law.
I am uncertain about the choice to make from the above laws for my nonlinear analysis; additionally I am uncertain about:
1. the values of the tangent modulus in Linear Hardening Law method,
2. the modified modulus and the exponent of strain in Power Law method, and
3. the Hardening Limit value in the Exponential Law.
Can you please help me with the above values and the reasons to use them? The material that I want to use is 4130 LHT with 80,000 psi Y.S.
Thank you in Advance,
Vikalp Luthra.
Hi Vikalp,
Difficult to answer you here without spending myself few hours plunging into engineering books.
So that’s what I’d advise you to do.
There are many books on material plasticity models.
Here’s an example:
https://www.amazon.com/Fundamentals-Theory-Plasticity-Mechanical-Engineering/dp/0486435830
It takes some time at the beginning, but once you understand the way nonlinear material calculates displacements and stresses, you will get a much better understanding of many topics related to nonlinear material modeling. A very useful investment of time.
Have fun ;-)