In today’s article, I am going to explore with you how to solve the simple cavity flow example with Openfoam!
This tutorial will describe how to pre-process, run and post-process a case involving isothermal, incompressible flow in a two-dimensional square domain.
Openfoam Lid-Driven Cavity Flow Tutorial
This is how the boundary conditions of the cavity are defined. All the boundaries of the square are walls. The top wall moves in the x-direction at a speed of 1 m/s while the other 3 are stationary.
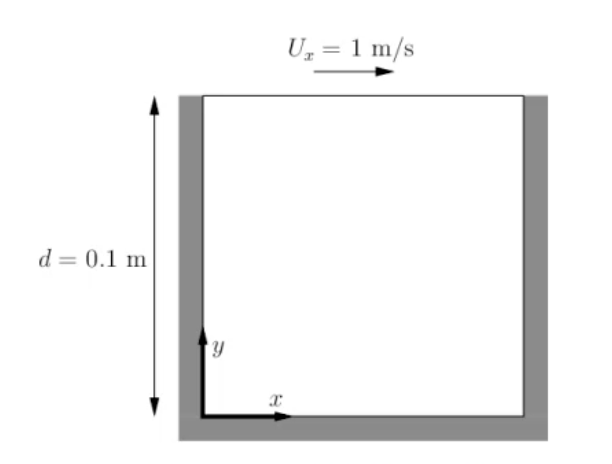
This example is fully detailed in open foam user guide here, so feel free to check it as well for the detailed process in text format.
If you like this kind of articles and if this is useful for you, please let me know in the comments!
I read every comment I get and I try to answer the questions as best as I can also ;-)
Happy New Year 2021 and Stay Safe!

Cyprien “Here comes the first Openfoam Tutorial!” Rusu
Hello Cyprien,
Youtube is replete with OpenFOAM tutorials. If possible, please see all that is there on internet and make tutorials for cases never discussed before. A suggestion would be to make tutorials on Fluid Structure Interaction using OpenFOAM and Code Aster or perhaps using foam extend version at https://openfoamwiki.net/index.php/Installation/Linux/foam-extend-4.1
which can handle Multi Degree of Freedom as well as FSI. If you like to have ideas, please have a look at http://www.tfd.chalmers.se/~hani/kurser/OS_CFD/
This site has projects and perhaps you can make video tutorials of the more difficult projects that are discussed there to get a better rating on youtube. Profile initialization, computational acoustics, programming in OpenFOAM or perhaps computational solid mechanics / finite element analysis using OpenFOAM or dealII might be a good idea.
Calculating the Courant number in OpenFOAM and visualize it in Paraview
Multiphase simulations mesh with cfMesh
Refining final mesh in only certain regions and only in certain directions
Adding streamlines during runtime
Plotting of averaged values on boundaries
Plotting of results at probe locations during run-time in transient simulations
Residual plotting in steady-state simulations
How to manipulate your inlet velocity fields (and any other field at a boundary)
How to calculate the Mach number in OpenFOAM and visualize it in Paraview
How to not skip zero time in Paraview
Initializing non-uniform fields
Defining additional boundaries
mesh with snappyHexMesh (some tutorials are not available but you can see where these tutorials are lacking)
Overset meshing with OpenFOAM
Plotting of averaged values on boundaries
If a simulation has run but one has forgotten to write the time steps, how to extract the time directories using bash commands without re-running the simulation
Regards,
Imad
Thanks for those ideas and links Imad! I will look into it.
I am doing simple videos first because there are still a lot of users who can benefit from it.
I don’t really care about the views on Youtube, I do that purely to teach engineering skills
(If I did care, I would probably have to switch to a gaming channel or doing slime videos like someone suggested in the youtube comments ;-) )
Hello, Cyprien!
First of all, happy New Year! I was looking with the great interest your Tutorial 2 (Lid-driven Cavity flow). I noticed you’re using Paraview ver 5.6.0, while my recent Ubuntu installation of OpenFoam8 on Ubuntu 16.04 LTS installed Paraview 5.4.0. Is there any big difference between these two versions and if any, how can I obtain th newer version of the Paraview? What concerns FSI, I would be also very much interested for these tutorials, especially those which are dealing with vibro-acoustic problems in compressible fluids (or aero-acoustics). Many thanks and regards!
Hi Neno,
Thanks for your message!
I don’t think there is much difference in the newest Paraview version for the average user… but if you are interested to know what changed, there are details here: https://blog.kitware.com/paraview-5-6-0-release-notes/
To install the newest preview version, you just have to uninstall the current version you have and install the last version from the Paraview website.
What kind of applications do you want to solve in vitro-acoustics?
FSI is generally a very complex to tackle (especially with open-source), but I know some specialised software that might be of some help depending of what you want to solve.
Hello, Cyprien!
Thank You for the grate explaining.
I have a question please:
I am solving the cavity tutorial with icoHeatFoam (the energy equation is added to icoFoam). I need to get the wallheaflux. when typing the command:
icoHeatFoam -postProcess -func wallHeatFlux
I got this error:
………………………………………………………………………………….
–> FOAM FATAL ERROR: (openfoam-2012)
Unable to find compressible turbulence model in the database
…………………………………………………………………………………
So, as I understand, it is not possible to get the wallHeatFlux while using a incompressible solver.
Then what to do?
I searched every where for a good answer but no help. Your help will be appreciated.
Hello, I am a master’s student trying to simulate the seismic wave behavior in the case of a cavitation layer in the ground at a depth of 2 meters. But I have a problem with inserting and programming the cavity part in the code using the Fortran program.
! subsurfacecavity.f90
!
! Cavity – Entry point of console application!
!Numerical Modeling of Surface Waves over Shallow Cavity
!SH_waves propagating in the xz plane,
! define dx(+) as forward derivative operator in x direction.
! define dx(-) as backward derivative operator in x direction.
! define dz(+) as forward derivative operator in z direction.
! define dz(-) as backward derivative operator in z direction
!Hereu(x, z,t) denotes the wave disturbance
!horizontal (lateral) coordinate x
!vertical(depth) coordinate z
! t is for the time.
!a(x, z)is for the medium velocity
!****************************************************************************
! u_x(z,x,t)=(1/dx)*[u(z,x+dx/2,t)-u(z,x-dx/2,t)] (1)
! u_z(z,x,t)= (1/dz)*[u(z+dz/2,x,t)-u(z-dz/2,x,t)] (2)
!u_x(z,x,t) = (1/sqrt(dz**2 + dz**2))*[u(z-dz/2,x+dx/2,t)-u(z+dz/2,x-dx/2,t)] (3)
!u_z(z,x,t) = (1/sqrt(dz**2 + dz**2))*[u(z+dz/2,x+dx/2,t)-u(z-dz/2,x-dx/2,t)] (4)
!u_x(z,x,t) = (1/2dx)*(u(z+dz/2,x+dx/2,t)-u(z-dz/2,x-dx/2,t)+u(z-dz/2,x+dx/2,t)-u(z+dz/2,x-dx/2,t)] (5)
!u_z(z,x,t) = (1/2dz)*(u(z+dz/2,x+dx/2,t)-u(z-dz/2,x-dx/2,t)-u(z-dz/2,x+dx/2,t)+ u(z+dz/2,x-dx/2,t)](6)
! calculate vx
!u(i,j,t)= 1/2*h(u(j+1,i+1,t)-u(j-1,i-1,t)+u(j-1,i+1,t)-u(j+1,i-1,t))
! calculate vz
!u(i,j,t)= 1/2*h(u(j+1,i+1,t)-u(j-1,i-1,t)-u(j-1,i+1,t)+u(j+1,i-1,t))
!****************************************************************************
program subsurfacecavity
implicit none
integer :: nx,nz,nt,ix,iz,lx,lz,i,j !area size
integer :: k0x,klx,k0z,klz
integer :: itrec
integer :: ixs,izs
integer :: it !Time loop variable
integer :: nmedia,b_x,b_z ! (Number media (layer,cavity)
integer :: present,next
integer :: xdir,zdir,forwrd,bckwrd
integer :: lop !Differential operator half length
parameter(lop=3) !lop=3Then the accuracy is 6th order
parameter(xdir=1,zdir=3,forwrd=0,bckwrd=1) !Parameters to calculate wave field components
real alpx(lop)
real alpz(lop)
real :: vp1,vs1,dens1 ! p-wave,s-wave, and density of Media_1
real :: vp2,vs2,dens2 ! p-wave,s-wave, and density of Media_2
real :: width,height !Dimension
real :: source_x,source_z ! source
real :: dx,dz,dt,dtrec !Spaces Steps
real :: layer,cavity
real :: delay,a1,a2,tmax !Delay time, tmax maximum cycle time
real :: fp ! Dominent Frequency(Source frequency)
real :: vzt1,vzt2
real :: snapshot_time,offset,interval
real :: vx_snapshot,vz_snapshot
real,parameter :: pi = 3.141592654
real,parameter :: twopi = 6.283185308
data alpx /1.20282,-0.08276,0.00950/ !Staggered Grid Finite Difference Coefficient
data alpz /1.20282,-0.08276,0.00950/ !Staggered Grid Finite Difference Coefficient
real, allocatable ,dimension(:,:,:) :: txx,tzz,txz,txx_x,txx_z,tzz_x,tzz_z,txz_x,txz_z !Define stress array, variable length
real, allocatable ,dimension(:,:,:) :: vx,vz,vx_x,vx_z,vz_x,vz_z !Define the particle velocity component array
real, allocatable ,dimension(:,:) :: w1,w2,dxx,dzz ! Buffer field value
real, allocatable ,dimension(:,:) :: lam,mu,twomu !Elastic parameters
real, allocatable ,dimension(:,:,:) :: rhoinv !density
real, allocatable ,dimension(:) :: src !Array of the function value of the hypocenter with respect to time
real, allocatable ,dimension(:) :: vxrec,vzrec !Array of particle velocity component values received by the geophone
integer, allocatable ,dimension(:) :: ixrec,izrec !Array of geophone positions
real, allocatable ,dimension(:,:) :: vp,vs,dens
integer nrec !nrec=2
!*********************** old File processing ********************
OPEN (888,file =”shallow cavity.txt”,STATUS=’OLD’)
READ(888,*)tmax,dtrec
READ(888,*)snapshot_time
READ(888,*)delay
READ(888,*)fp
READ(888,*)nmedia
READ(888,*)vp1,vs1,dens1
READ(888,*)vp2,vs2,dens2
READ(888,*)width,height
READ(888,*)source_x,source_z
READ(888,*)dt,dx,dz
READ(888,*)nrec,offset,interval
READ(888,*)b_x,b_z
! recording of particle velocities at nrec stations
allocate(vxrec(nrec),vzrec(nrec))
allocate(ixrec(nrec),izrec(nrec))
! grid size
nx=width/dx+1
nz=height/dz+1
allocate(vp(nx,nz),vs(nx,nz),dens(nx,nz),lam(nx,nz),twomu(nx,nz),mu(nx,nz),rhoinv(nx,nz,2))
! grids
do ix=1,nx
do iz=1,12/dz
vp(ix,iz)=vp1
vs(ix,iz)=vs1
dens(ix,iz)=dens1
lam(ix,iz)=dens(ix,iz)*(vp(ix,iz)**2-2.0*vs(ix,iz)**2)*dt
mu(ix,iz)=dens(ix,iz)*(vs(ix,iz)**2)*dt
twomu(ix,iz)=2.0*mu(ix,iz)
rhoinv(ix,iz,1)=dt/dens(ix,iz)
enddo
do iz=12/dz+1,nz
vp(ix,iz)=vp2
vs(ix,iz)=vs2
dens(ix,iz)=dens2
lam(ix,iz)=dens(ix,iz)*(vp(ix,iz)**2-2.0*vs(ix,iz)**2)*dt
mu(ix,iz)=dens(ix,iz)*(vs(ix,iz)**2)*dt
twomu(ix,iz)=2.0*mu(ix,iz)
rhoinv(ix,iz,1)=dt/dens(ix,iz)
enddo
enddo
! p-wave velocity, s-wave velocity and density
! vp=888.0
! vs=431.0
! dens=1600
!*********************** output files ********************
open(unit=11,file=”vx_kgs.txt”)
open(unit=12,file=”vz_kgs.txt”)
open(unit=15,file=”vx_snapshot.txt”)
open(unit=16,file=”vz_snapshot.txt”)
! source position
ixs=source_x/dx+1
izs=source_z/dz+1
! receiver position
do i=1,nrec
ixrec(i)=ixs+offset+(i-1)*interval
izrec(i)=1
enddo
! time stepping and sampling interval for recording
itrec=nint(dtrec/dt)
nt=nint(tmax/dt)+1
! source time function.
allocate(src(nt))
!source time function is first derivative of gaussian.
!parameterization is the same as for analytical calculation
a1=-twopi*fp*exp(0.5)
a2=-0.5*(twopi*fp)**2
call gauss(src,nt,dt,delay,a1,a2)
! derivative operator half lengths
lx=lop
lz=lop
! the dynamic (time dependent) fields have buffer areas for “ix nx”, “iz nz”.
k0x=-(lx-1) !k0x=-2
klx=nx+lx !klx=404
k0z=-(lz-1) !k0z=-2
klz=nz+lz !klz=204
! dynamical fields
allocate(txx(k0x:klx,k0z:klz,2),tzz(k0x:klx,k0z:klz,2),txz(k0x:klx,k0z:klz,2))
allocate(vx(k0x:klx,k0z:klz,2),vz(k0x:klx,k0z:klz,2),dxx(1:nx,1:nz),dzz(1:nx,1:nz))
allocate(vx_x(k0x:klx,k0z:klz,2),vx_z(k0x:klx,k0z:klz,2),vz_x(k0x:klx,k0z:klz,2),vz_z(k0x:klx,k0z:klz,2))
allocate(txx_x(k0x:klx,k0z:klz,2),tzz_x(k0x:klx,k0z:klz,2),txz_x(k0x:klx,k0z:klz,2))
allocate(txx_z(k0x:klx,k0z:klz,2),tzz_z(k0x:klx,k0z:klz,2),txz_z(k0x:klx,k0z:klz,2))
! work arrays for dynamical fields
allocate(w1(k0x:klx,k0z:klz),w2(k0x:klx,k0z:klz))
! initial conditions
txx=0.0
txx_x=0.0
txx_z=0.0
tzz=0.0
tzz_x=0.0
tzz_z=0.0
txz=0.0
txz_x=0.0
txz_z=0.0
vx=0.0
vz=0.0
vx_x=0.0
vx_z=0.0
vz_x=0.0
vz_z=0.0
w1=0.0
w2=0.0
vxrec=0.0
vzrec=0.0
! spatial step lengths
layer=b_x*dx
! make derivative operators dependent of step length
alpx=alpx/dx
alpz=alpz/dz
! free surface:(Free interface parameter setting)
lam(1:nx,1)=0.0
twomu(1:nx,1)=0.5*twomu(1:nx,1)
rhoinv(1:nx,1,1)=2.0*rhoinv(1:nx,1,1)
! time integration of elastic fields
do it=1,nt !Time loop
present=mod(it+1,2)+1 !Take the remainder
next=mod(it,2)+1 !Take the remainder
do iz=1,nz
do ix=1,nx
dxx(ix,iz)=0.0
dzz(ix,iz)=0.0
if(ix.le.(1+layer/dx))then
dxx(ix,iz)=(2*vp(ix,iz)/layer)*log(1/0.0001)*((1+layer/dx-ix)*dx/layer)**4
endif
if(ix.ge.(nx-layer/dx))then
dxx(ix,iz)=(2*vp(ix,iz)/layer)*log(1/0.0001)*((ix-(nx-layer/dx))*dx/layer)**4
endif
if(iz.ge.(nz-layer/dz))then
dzz(ix,iz)=(2*vp(ix,iz)/layer)*log(1/0.0001)*((iz-(nz-layer/dz))*dz/layer)**4
endif
enddo
enddo
! calculate vx
call der(xdir,bckwrd,txx(k0x,k0z,present),w1,nx,nz,alpx,lx,k0x,klx,k0z,klz)
vx_x(1:nx,1:nz,next)=((1-0.5*dt*dxx(1:nx,1:nz))/(1+0.5*dt*dxx(1:nx,1:nz)))*vx_x(1:nx,1:nz,present)&
+(1/(1+0.5*dt*dxx(1:nx,1:nz)))*rhoinv(1:nx,1:nz,1)/dx*w1(1:nx,1:nz)
call der(zdir,bckwrd,txz(k0x,k0z,present),w2,nx,nz,alpz,lz,k0x,klx,k0z,klz)
vx_z(1:nx,1:nz,next)=((1-0.5*dt*dzz(1:nx,1:nz))/(1+0.5*dt*dzz(1:nx,1:nz)))*vx_z(1:nx,1:nz,present)&
+(1/(1+0.5*dt*dzz(1:nx,1:nz)))*rhoinv(1:nx,1:nz,1)/dx*w2(1:nx,1:nz)
vx(1:nx,1:nz,present)=vx_x(1:nx,1:nz,present) + vx_z(1:nx,1:nz,present)
vx(1:nx,1:nz,next)=vx_x(1:nx,1:nz,next) + vx_z(1:nx,1:nz,next)
! calculate vz
call der(xdir,forwrd,txz(k0x,k0z,present),w1,nx,nz,alpx,lx,k0x,klx,k0z,klz)
vz_x(1:nx,1:nz,next)=((1-0.5*dt*dxx(1:nx,1:nz))/(1+0.5*dt*dxx(1:nx,1:nz)))*vz_x(1:nx,1:nz,present)&
+(1/(1+0.5*dt*dxx(1:nx,1:nz)))*rhoinv(1:nx,1:nz,1)/dx*w1(1:nx,1:nz)
call der(zdir,forwrd,tzz(k0x,k0z,present),w2,nx,nz,alpz,lz,k0x,klx,k0z,klz)
! add directional force in z-direction to w2
call addfz(w2,src(it),ixs,izs,nx,nz,dx,dz,k0x,klx,k0z,klz)
vz_z(1:nx,1:nz,next)=((1-0.5*dt*dzz(1:nx,1:nz))/(1+0.5*dt*dzz(1:nx,1:nz)))*vz_z(1:nx,1:nz,present)&
+(1/(1+0.5*dt*dzz(1:nx,1:nz)))*rhoinv(1:nx,1:nz,1)/dx*w2(1:nx,1:nz)
vz(1:nx,1:nz,present)=vz_x(1:nx,1:nz,present) + vz_z(1:nx,1:nz,present)
vz(1:nx,1:nz,next)=vz_x(1:nx,1:nz,next) + vz_z(1:nx,1:nz,next)
! recording: (Record the particle velocity component, call the recording sub-function, and output the recorded value)
call recordata(vx,vz,vxrec,vzrec,ixrec,izrec,nrec,nx,nz,k0x,klx,k0z,klz)
if(mod(it,itrec).eq.1) then
do i=1,nrec
write(11,*) vxrec(i)
write(12,*) vxrec(i)
enddo
endif
! change by yxz
if(it.eq.nint(snapshot_time/dt))then
do ix=1,nx
do iz=1,nz
vx_snapshot=0.5*(vx(ix,iz,1)+vx(ix,iz,2))
if(iz.eq.1)then
vzt1=0.25*(vz(ix-1,iz,1) + vz(ix,iz,1))
vzt2=0.25*(vz(ix-1,iz,2) + vz(ix,iz,2))
vz_snapshot=0.5*(vzt1+vzt2)
else
vzt1=0.25*(vz(ix-1,iz-1,1) + vz(ix,iz-1,1) &
+ vz(ix-1,iz,1) + vz(ix,iz,1))
vzt2=0.25*(vz(ix-1,iz-1,2) + vz(ix,iz-1,2) &
+ vz(ix-1,iz,2) + vz(ix,iz,2))
vz_snapshot=0.5*(vzt1+vzt2)
endif
write(15,*) ix,iz,vx_snapshot
write(16,*) ix,iz,vz_snapshot
enddo
enddo
endif