Buckling in FEA: A simple explanation and demonstration

Hundreds of engineers asked me about buckling and every time, the way that I explain it makes them understand almost immediately how it works.

That’s what I’ll share with you today for the beginning of 2017 :)

Buckling is very simple to understand with the simple following example.

Imagine that you are pushing a parallelepipedic shape of metal with both hands on each end.

Will you ever be able to break it?

I am sure that you guessed by experience that you won’t…

But why?

Simple…

The load that you apply with your hands will never cause enough stress to exceed the material resistance that will make it yield.

Or said simply: You are not strong enough.

Second question:

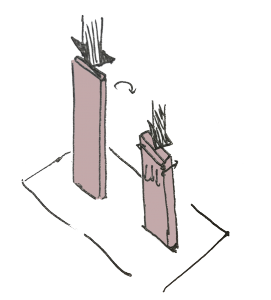
Suppose that I just change one parameter in this experiment… I decide to reduce the thickness of my parallelepipedic shape to 0.5 mm

You now have something which looks exactly like a ruler in your hands

What happens now if you apply exactly the same pressure on both sides with your hands?

Do you have the confidence that you can break it now?

Why is that?

The material is the same, the load is the same, applied in the same direction right?

The answer is simple…

This time, it breaks not because the loads exceeded the maximum stress resistance.

It breaks because another phenomenon linked to the geometry of the part….

And it happens for all the parts that have a small thickness (typically…shells)

This phenomenon is called buckling.

So, without knowing it, we all have at least once buckled and broken a ruler in our chilhood (several in my case ;-) )

How do you explain failure by Buckling?

Let’s go back to the experiment and think hard.

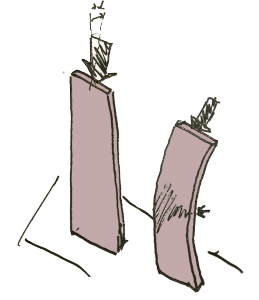
If you take a ruler and apply a load exactly in the same plane on both sides and if you suppose that the load is a perfect linear load with a perfect orientation…. will it break the ruler?

In theory, no.

It should compress, and the cross section should change a bit due to the poisson’s effect.

(That’s why…when you do a linear static analysis you will see exactly that and you won’t observe the buckling. We’ll see that in the video below)

But in practice, yes!

Buckling is something in relation with the difference between classic linear static theory and reality here.

We suppose the load had a perfect orientation…

In reality, in almost never happens (Perfection only exists in our heads and in formulas we created from models).

There is always a very small, almost insignificant +α of the load in another direction.

This +α is what creates an instability in the system and causes the ruler to buckle.

Because more you push and more the +α becomes important… so important in fact that it causes the ruler to break MUCH before it’s material resistance limit.

Why is buckling so dangerous?

Think about it for one second.

You built a system which is theoretically okay.

You tested all the loading scenarios and every light is green. It will never fail.

Then…

Someone using your product doesn’t calibrate right how the system is fixed… maybe he fixes it on a ground which is not exactly horizontal… even with a 0.5 mm of difference.

And your wonderful system starts to buckle and fails.

Wouldn’t that be dangerous?

The guy will probably be angry and will start to call the support service to get back his money quickly…

You can tell him that you checked everything and everything was perfectly okay in your testing conditions and inside your computer model.

Will he listen? Probably not.

Maybe there will even be lives on the line.

If the system is something huge like a crane or a structural element of a building… then it becomes really dangerous.

Yep, buckling is something serious man…

How to calculate the buckling load for a simple pin-joined elastic beam

With a so dangerous failure mode creating so much potential damage, you guess that engineers have been developing models over time to try to calculate what really happens.

For a simple beam with a very small thickness, what happens is clear like water.

What we want to know is the minimum load that will cause buckling to happen.

We generally call it the lowest buckling load.

(Why “lowest”, we’ll see that in an instant…)

This load is important because it causes failure much BEFORE the usual material failure.

There are several ways to do the calculation, but I’d like to show you one of them called the adjacent equilibrium method.

In this method, the buckling load is calculated by considering a slightly bent configuration of a pinned-pinned elastic beam.

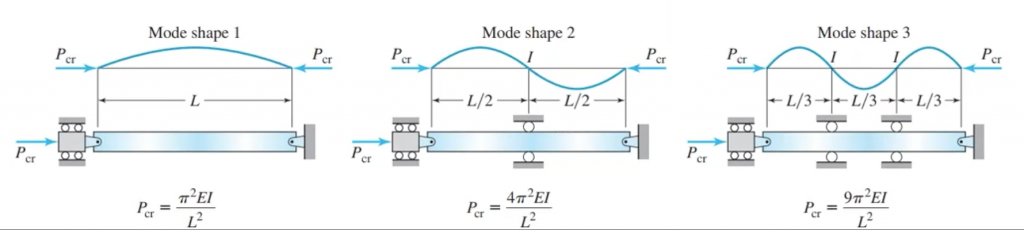
Why are there several buckling modes?

You saw that I took n=1 in the previous example, that’s because I calculated the buckling load of the first buckling mode, also called the lowest or fundamental buckling load.

There are other buckling modes… everything depends on how your beam is constrained.

If it is prevented to buckle with the shape of the first buckling mode because it is prevented to do so by a pin for example, then it will still buckle, but along the second buckling mode.

How to do buckling in FEA?

I almost forgot this blog is about FEA :)

Linear Buckling in FEA is actually very simple

(Nonlinear buckling is much more tricky…)

Here’s the video:

Is there more to know about buckling?

You bet there is :)

As always… when you start to understand something, you discover there’s plenty more things to understand about it that you weren’t aware of!

This article gives a very simple explanation of the concept but there are much more things to know about buckling.

For example, there is linear and nonlinear buckling…

I talked about it in a webinar I did previously, you can watch it here if you are interested

That’s all for today!

/////////////////////////////////////////////////////

You maybe noticed that I wrote a lot of great educational article… that’s because I really want to contribute and help engineers who are new to FEA to understand those concepts better and faster!

I am not hiding that it takes a lot of efforts to write all that, so…

If you like this article, there are 3 things you can do for me:

1- Help me to share this article on Linkedin, facebook, twitter or in your habitual forum to help more people understand buckling (use the share button on the left of the article).

2- Let me know in the comments what you learned from it and what you would like to learn even further so I can write more on the topic

3- Join the newsletter (if you are not already subscribed), I’ll send you everything I write (and much more) by email!

Thank you for reading!

–Cyprien