How to use Weibull Law to identify a better rupture criterion for Brittle Materials? (Part 1)

Today, Let’s talk about some basics of ductile and brittle materials… and how you can find an appropriate failure criteria for brittle materials with defects!

I registered an audio file to make it more easy to understand, I hope this subject will interest you!

1 Rupture criterions for ductile and brittle materials

Usually, when we worked a lot with steel material which is a fully homogeneous and ductile material,
We tend to want to transpose the way we generally talk about Failure in other types of materials

For example, If I know that at 700 MPa, my steel will fail, I can say that as long as my Von Mises stress stays below 700 MPa, my steel is safe against failure and the rupture criteria then can be written as:

$\sigma_{F} < 700 MPa$

Unfortunately, it is very difficult to apply the same logic to brittle materials.

2 Brittle materials, defects and homogeneity

Just a quick reminder:

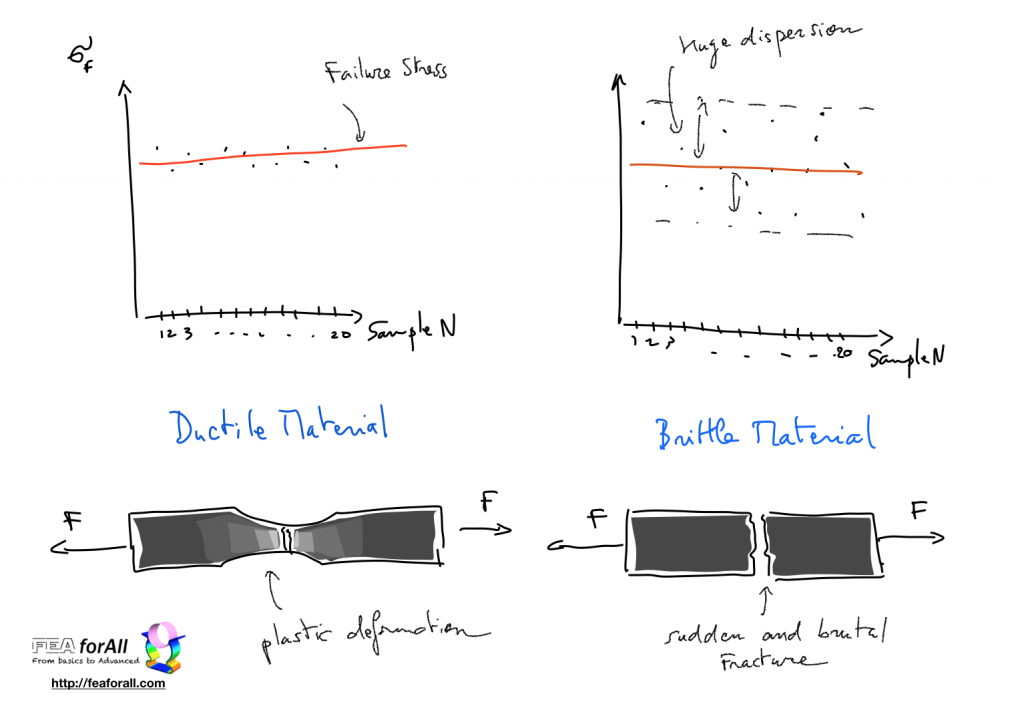
Ductile materials are materials like steel which deform plastically and break only after a certain ultimate load is reached.

Brittle material (like Concrete or glass) do not deform plastically, they usually fail and break very brutally.

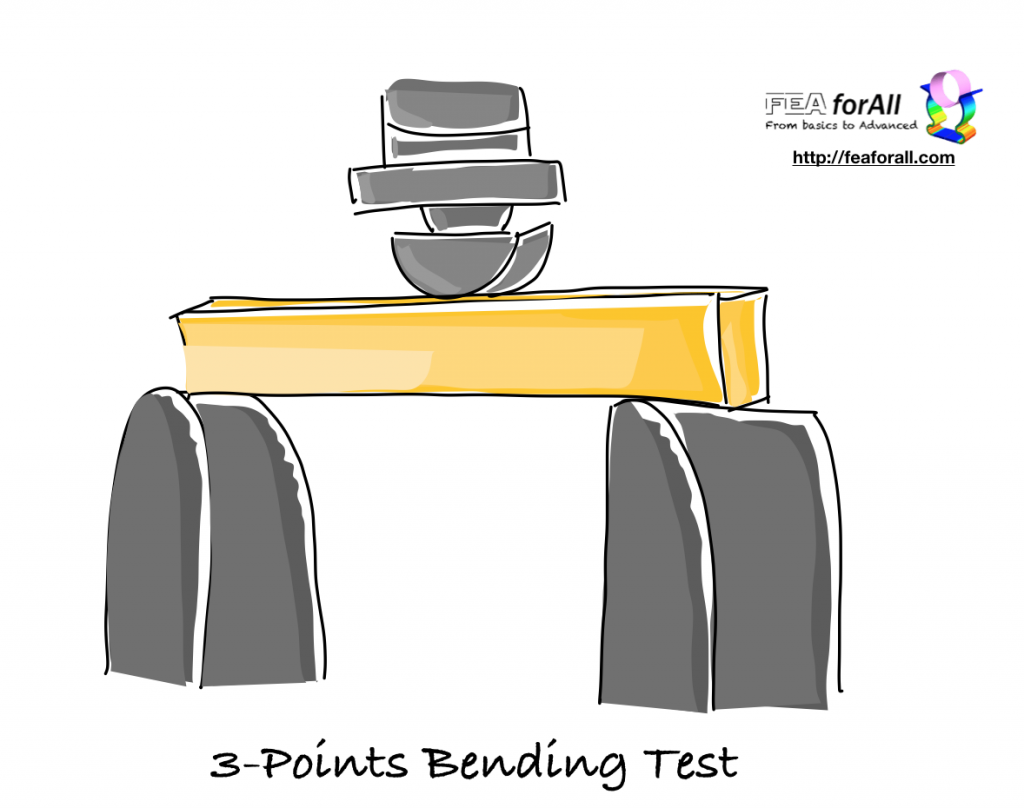
Let’s now perform a small experiment which will help us to understand how to develop a failure criteria for a brittle material such as concrete

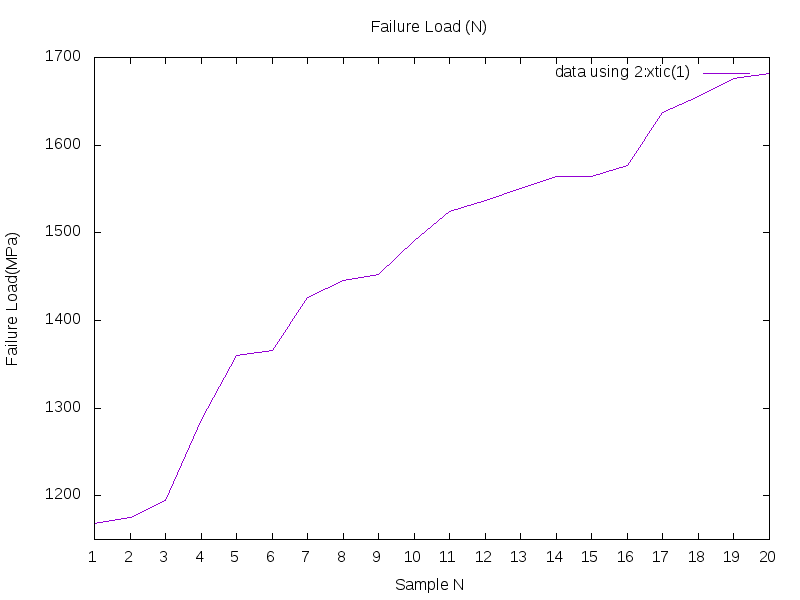
If we tried to perform a 3 points bending test to a series of ~20 concrete material 2cm x 2cm x 8 cm samples, we would note a big dispersion in the value we obtain for the failure loading.

And Yes, it’s yellow, but it is concrete material ;-)

Here I list the result of the 20 experiments sorted by the value of the failure Load

Sample N	Failure load(N)
1	1168
2	1175
3	1195
4	1287
5	1360
6	1366
7	1426
8	1445
9	1452
10	1491
11	1524
12	1537
13	1551
14	1564
15	1564
16	1577
17	1637
18	1656
19	1676
20	1682

As we can see here, the dispersion in the results obtained is quite huge.

What happens is that brittle materials have defects which are in variable quantity and size
Those defects leads to the fact that the “homogeneity hypothesis” doesn’t necessarily apply as well for such brittle materials with different kind of defects

If we chose a simple beam model, we can easily calculate the failure stress from the applied loading

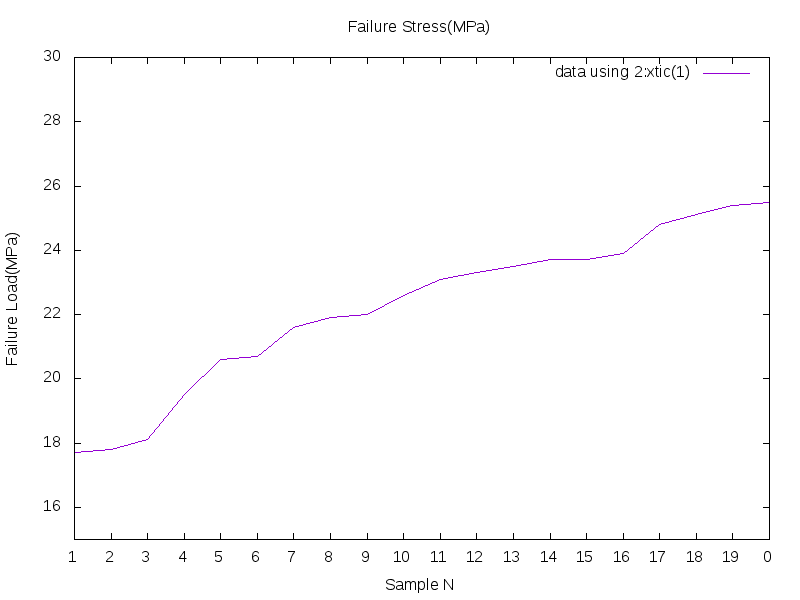
We then get the failure stress distribution which has a huge dispersion of values displayed in teh table below:

N	Sigma Failure(MPa)
1	17.7
2	17.8
3	18.1
4	19.5
5	20.6
6	20.7
7	21.6
8	21.9
9	22
10	22.6
11	23.1
12	23.3
13	23.5
14	23.7
15	23.7
16	23.9
17	24.8
18	25.1
19	25.4
20	25.5

This proves that the hypothesis of homogeneous material taken is wrong
(because all the samples are geometrically identical and made from the same material, but obtained results display huge differences)

3 The probabilist model of material failure: The Weibull criteria

As the type of simple inequality criteria we used for steel is not valid anymore, we have to find another kind of criteria to describe the condition of failure.

This criteria should help us to:

Predict the distribution of stresses at failure
Be identifiable with experiments (at a good cost)

Fracture mechanics tells us that the failure of brittle materials is essentially caused by the size and quantity of defects in the material.

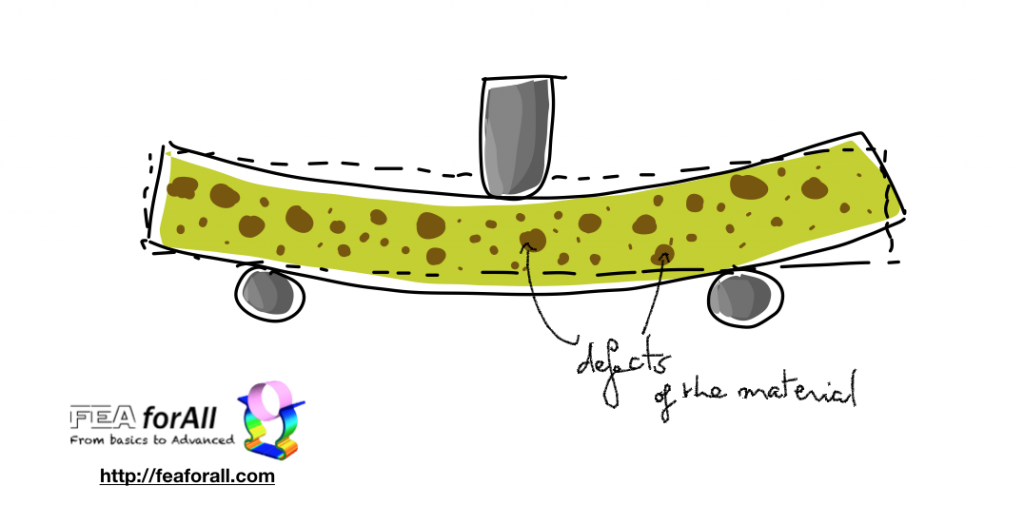
Because of that, we don’t really have to determine very precisely the stress distribution at every point of the solid (This would be an overkill)

We just need to find a criterial which relates the failure with the size and the quantity of defects.

4 The Weibull Criteria

The Weibull criteria is a criteria which provides the probability of rupture of a material under a certain stress value.

To give an example of what is a probabilist failure criteria:

Instead of saying:

If Stress > 20 MPa, the material fails (Deterministic)

We say

If Stress > 20 MPa, the material has 20% chances of failure (Probabilist)

Such probabilist failure criteria is generally used in Fatigue Analysis

5 Hypothesis we can take

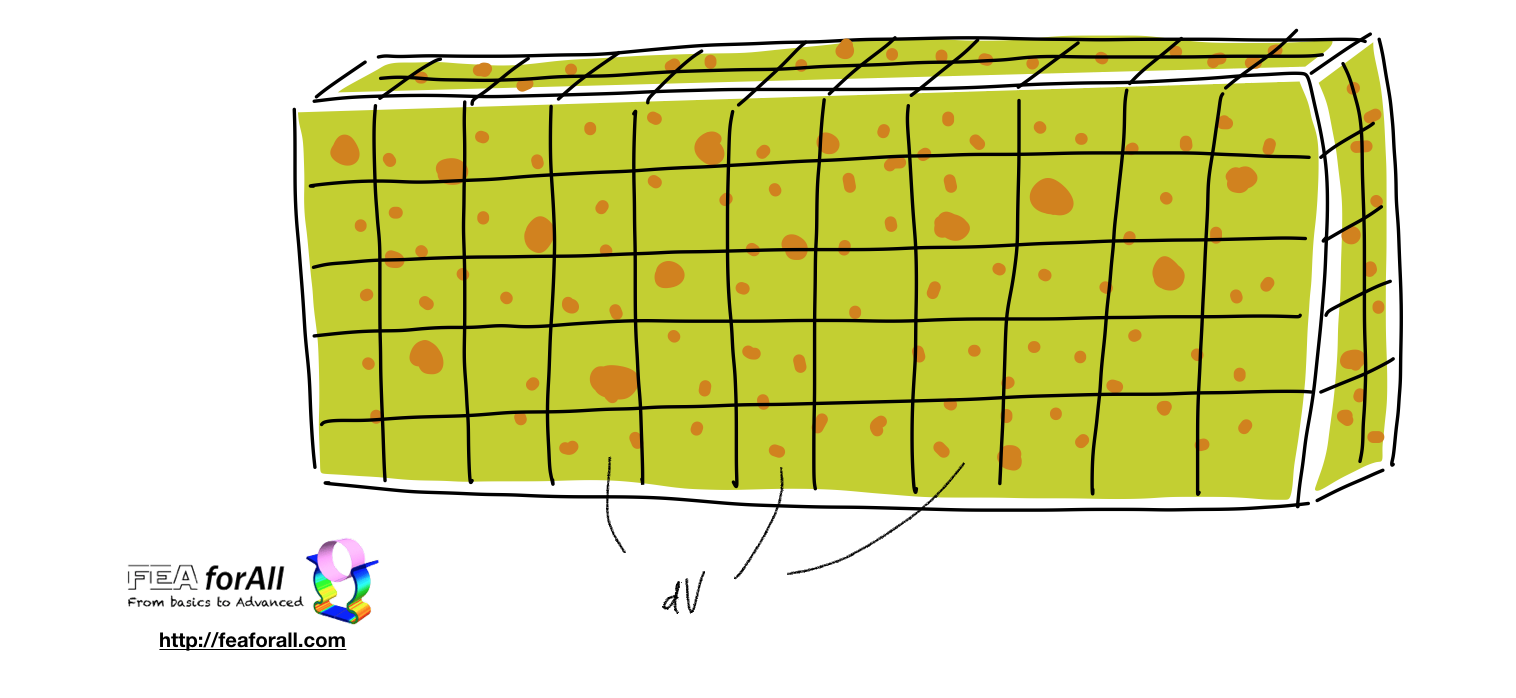
If we consider that our volume is composed by an infinite number of small volumes dV

We associate to each dV a certain failure resistance (and we suppose each volume is independant with another)

Each dV has a certain amount of defects in various quantities and sizes inside it

In function of the state of stress in dV, the defects can be activated or not

Then, as soon as one of the defects in a dV is activated, we consider it leads to the failure of the whole part.

6 The probabilistic model

We want now to answer this question:

What is the probability that a defect will be activated in a small dV?

We can choose a law of Poisson to represent this probability
(because this law is usually used to count the number of punctual events)

The probability to find k defects activated in a volume V can then be written as:

$P_{k}(V)=\frac{(\lambda V)^{k}}{k!} e^{- \lambda V}$

λ corresponds to a density of activation of defects under a given load.
k is an integer variable which gives the number of activated defects.
We should understand here that as long as k remains =0, the sample survives and when k>1, it means we have at least one defect and this leads to failure.

7 Calculating the parameters of the model

Weibull chose to represent lambda as a power distribution:

$\lambda=\frac{1}{V_{0}} \times \Big(\frac{ \sigma }{ \sigma _{0} }\Big)^{m}$

more the stress σ increases and more the density of activated defects λ increases.
m is a parameter called the “Weibull Module” which models the dispersion of lambda
The other 2 parameters V0 and sigma0 are in fact not independent and we can only try to determine one of them called the scale factor:

$\sigma_{0}*V_{0}^{1/m}$

which can be understood as the average activation stress

If we mix all that with the Poisson’s Law, we get the probability of failure Pf:

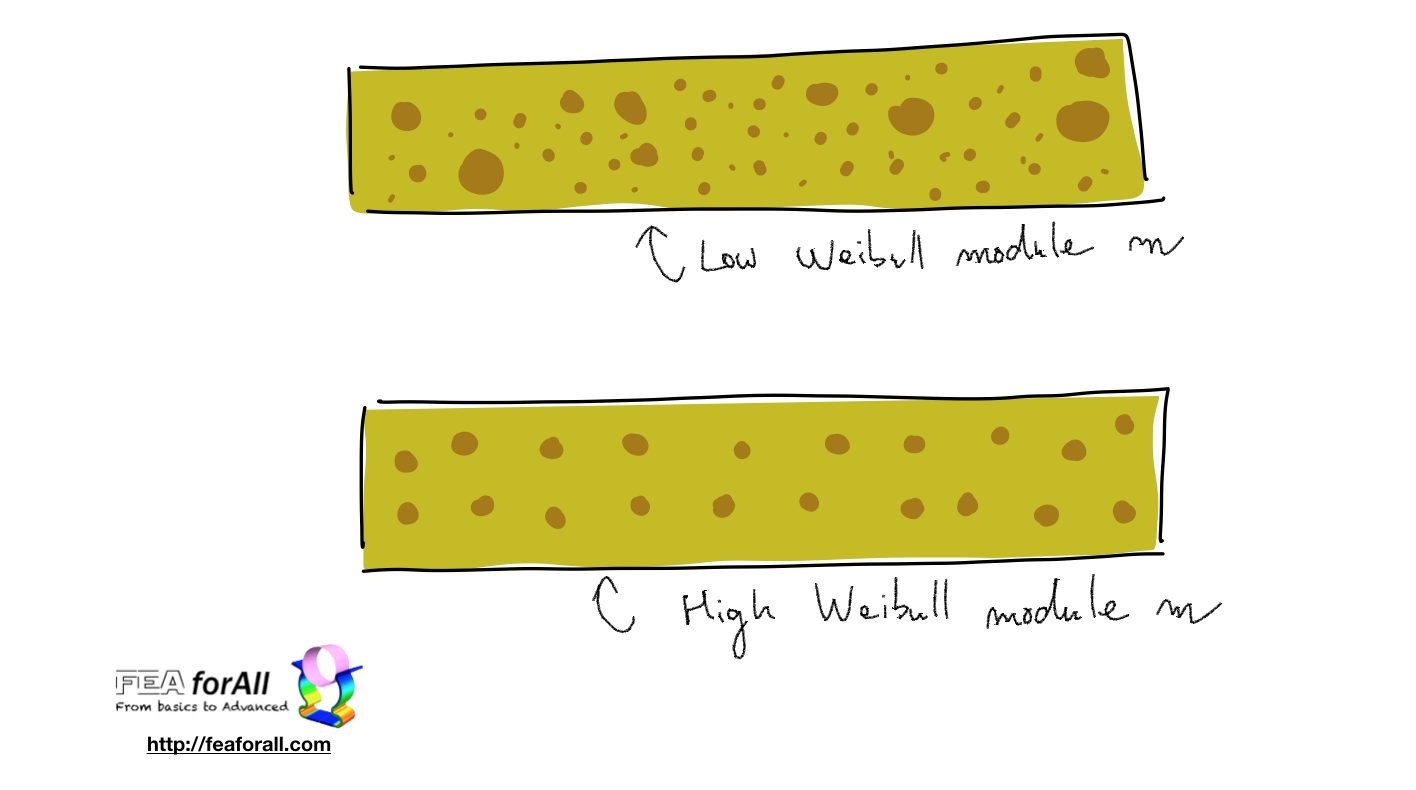
$P_{f} = 1-P_{s} = 1- exp \Big[\frac{-V}{V_{0}} \Big(\frac{\sigma}{\sigma_{0}}\Big)^{m} \Big]$

The Weibull module m is material parameter which characterise the distribution of defects in the material.

if m is small, it means there is a lot of different kind of defects (in size and place)

if m is high, defects will tends to be similar in size and well distributed.

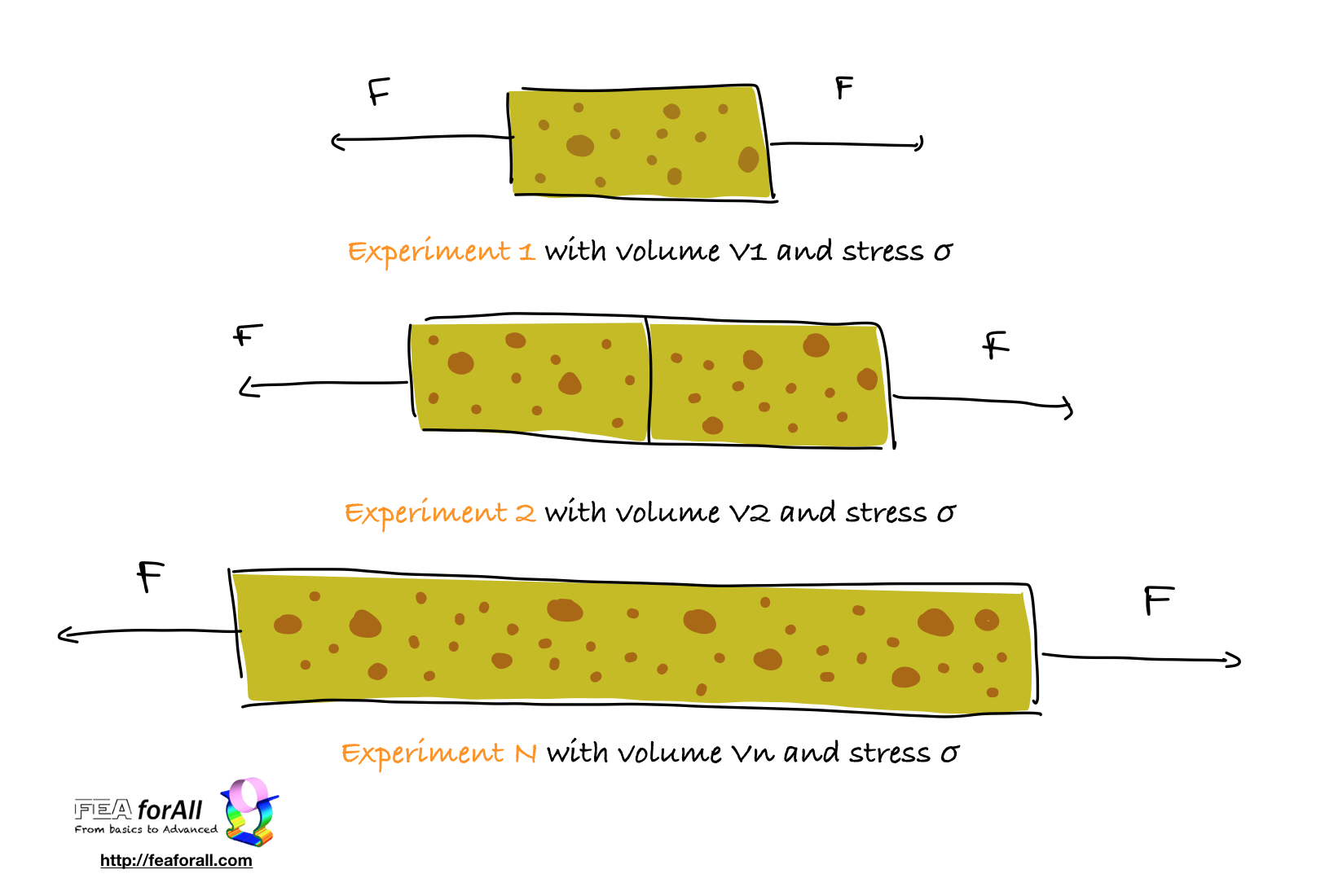
8 The influence of the volume

Brittle materials generally have the following property:
The larger the Volume, the higher is the probability to have a big defect inside it.

It means that we are more likely to find big defects leading to faster brittle failure in larger volumes.

As an example to consider the influence of the volume, we can consider the following situation:

We take one sample and we apply a load F, it has a probability of non-failure of
$(1-P_{f})$

If we double the size of the volume but keep the same load F, the probability of failure is now
$(1-P_{f})*(1-P_{f})$

The probability of non-failure of a sample composed of n such volumes would be:
$1-P_{fn} = (1-P_{f})*(1-P_{f})*.....*(1-P_{f})= (1-P_{f})^{n}$

If we take the log:

$log(1-P_{fn}) = n \times log(1-P_{f})$

The probability of failure of a sample of volume V is thus linked to the probability of failure of a sample of volume V0 with the formula:

$log(1-P_{f})=\frac{V}{V_{0}} \times log(1-P_{f_{0}})$

9 The influence of loading

Until now, I considered that the loading caused an uniform stress in all the sample.

But actually, it is clear that it is not always the case.

The probability of failure is higher when the defects are activated in a zone of higher stress.

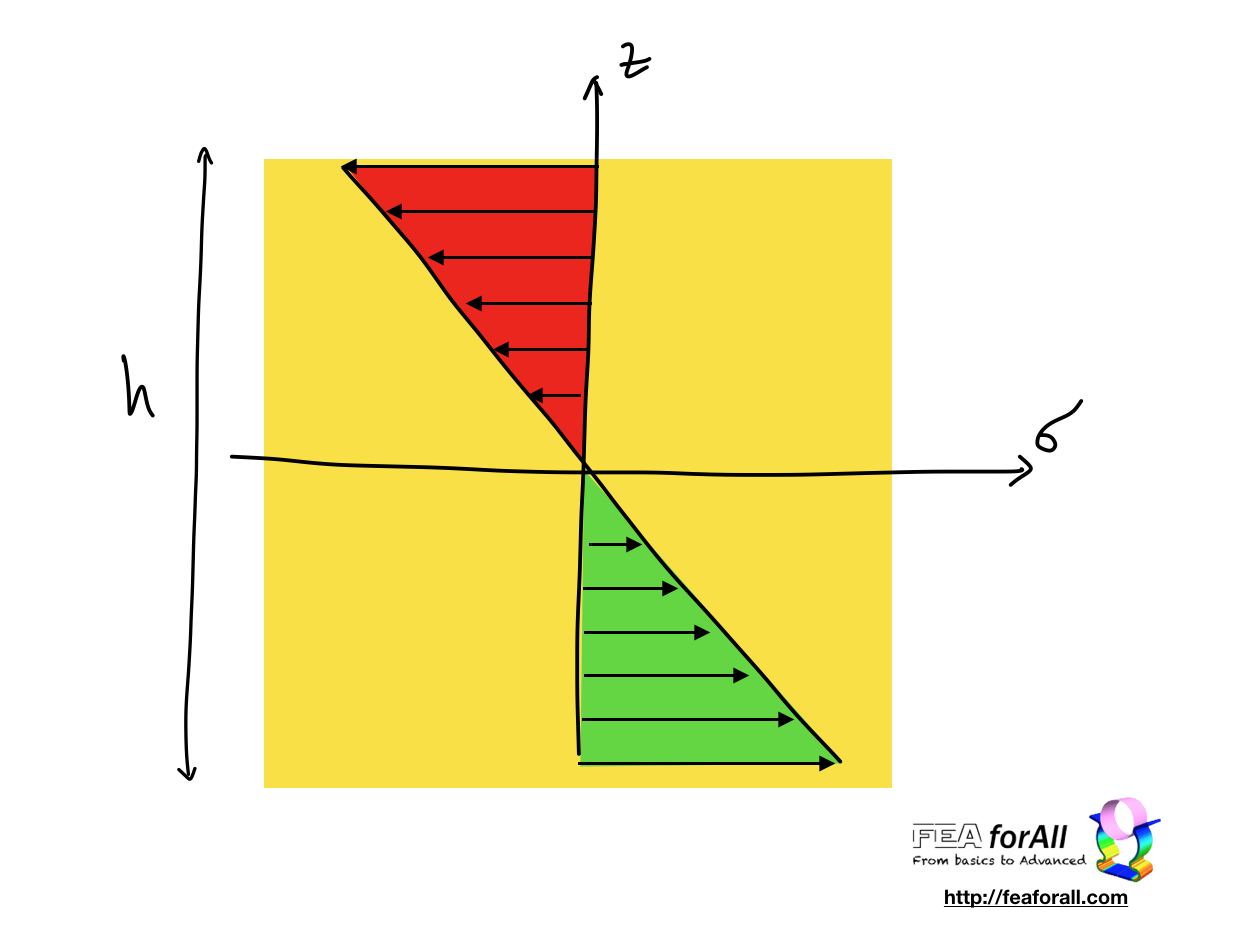
We can use a parameter H to represent the heterogeneity of stresses and thus replace the volume by:

$V_{eff} = V.H$

V_eff represent the volume of a sample which, submitted uniformly to the maximum stress, would have the same probability of failure than the real part.

$V_{eff}=\int_V \frac{\langle \sigma \rangle}{\sigma_{F}} dV$

For such sample of volume V in an heterogeneous state of stress, the probability of Failure would be written:

$P_{f}=1-exp \Big[- \frac{V_{eff}}{V_{0}} \Big(\frac{\sigma_{F}}{\sigma_{0}} \Big)^{m} \Big]$

10 Numerical Application

Check this article for the numerical application.

I’ll explain how to use Python to calculate the parameters of the Weibull Law:

How to determine Weibull Law Parameters with Python? (Part 2)

That’s all for today, hope you understand better now how to use the Weibull criteria to identify the failure stress of brittle material

Obviously, there is more to know about this topic… but that will be for next time!

–Cyprien

PS: If you like what I write, subscribe to the newsletter and help me to spread the knowledge by sharing this article! We all win by learning from each other and making the engineering knowledge more accessible :-) THANK YOU!

Comments

Angus Ramsay says

December 10, 2018 at 9:06 am

Always good to read you posts Cyprien. One thing that you might like to note is that when concrete is under reinforced then it does behave in a ductile manner with one of the failure modes being plastic collapse – think of the yield line technique etc. Angus.

Sukumar Baishya says

December 10, 2018 at 9:43 am

Beautiful presentation of the basic concepts pertaining to an important model commonly used in various areas of engineering. Thank you for sharing. Would look forward to go through the 2nd part.
Best wishes and regards.

Sergio Pluchinsky says

December 10, 2018 at 11:39 am

Really interesting post. I have done a few weeks ago some simulations on cast iron parts (gas compressor cilinders) and was hard to explain to my customer that he must be very carefull even if he was well bellow the specified yield stress values. The same about more defect on big volumes areas, cast parts must be designed to have the more constant thikness as possible to avoid such concentration of deffects (air trapped).

Best regards, and keep posting such usefull information!

Nasseh says

December 10, 2018 at 11:43 am

This was useful. Thanks for sharing. Please write the second part.

Sagar says

December 10, 2018 at 11:50 am

Great Content.
Keep Posting.

Chris Schaefer says

December 10, 2018 at 12:54 pm

Cyprien,
A very good introduction to brittle failure! Thank You for sharing.

harsha says

December 10, 2018 at 1:55 pm

very good article, it paved an another way for me to think how I give FEA results for my cast iron analysis. thank you for good post.

Zhi Lu says

December 10, 2018 at 2:09 pm

Ever tried to simulate bending a spaghetti? it will break into more than two pieces every time, unless you twist it before banding. It will be a good case if you can use FEA to show the same.

:)

Rameez FAROUK says

December 10, 2018 at 9:05 pm

Cyprien,
Good work, keep posting it. It’s is really helpful for beginners to have idea of topics which are quite different from the academic. I am waiting for the part 2. All the best. Cheers

Steve Gavin says

December 10, 2018 at 11:07 pm

Thank you for sharing this article.
I am working with grey cast iron which behaves as a brittle material due to the carbon flake size and form. Also temperature affects UTS. It can be quite complicated to replicate test results with FEA.

Sanjay Kumar yadav says

December 11, 2018 at 2:33 pm

Thank you sir.keep posting sir

Sanjay Kumar yadav says

December 11, 2018 at 2:53 pm

Thank u sir .plz send it is helpful

GiancarloAV8 says

December 20, 2018 at 9:46 pm

I would like to contact you, I am having a lot of problems with a geometry in salome, I would like taht you help me.

Yury says

December 22, 2018 at 9:29 am

Great Idea of concrete fracture simulation. It looks like non-local failure theory implemeted in LS-DYNA. But now we have new challenges: how to determent probably parameter?